Question

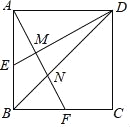
【题目】正方形ABCD的边长AB=2，E为AB的中点，F为BC的中点，AF分别与DE、BD相交于点M，N，则MN的长为（　　）

A. B. ﹣1 C. D.

Answer 1

【答案】C

【解析】

首先过F作FH⊥AD于H，交ED于O，于是得到FH=AB=2，根据勾股定理求得AF，根据平行线分线段成比例定理求得OH，由相似三角形的性质求得AM与AF的长，根据相似三角形的性质，求得AN的长，即可得到结论．

解：过F作FH⊥AD于H，交ED于O，则FH=AB=2，

∵BF=FC，BC=AD=2，
∴BF=AH=1，FC=HD=1，

∴AF= = = ,

∵OH∥AE，

∴ ,

∴OH= ,

∴OF=FH-OH=2- = ,

∵AE∥FO，
∴△AME∽FMO，

∴ ,

∴AM=AF= ,

∵AD∥BF，
∴△AND∽△FNB，

∴ ,

∴AN=2NF= ,

∴MN=AN-AM= .

故选：C．