题目内容
16.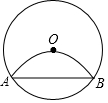 如图,线段AB是⊙O的弦,点P在⊙O上(点P不与点A、点B重合),连接AP、BP,若将⊙O沿弦AB折叠,圆弧恰好经过圆心O,则∠APB的大小为60°或120度.
如图,线段AB是⊙O的弦,点P在⊙O上(点P不与点A、点B重合),连接AP、BP,若将⊙O沿弦AB折叠,圆弧恰好经过圆心O,则∠APB的大小为60°或120度.
分析 作OD⊥AB于D,交⊙O于C,连接OA、OB、AC、BC,如图,利用折叠性质得AB垂直平分OC,则利用垂径定理得到OC垂直平分AB,所以可判断四边形ACBO为菱形,易得△AOC和△BOC都是等边三角形,则∠AOC=∠BOC=∠ACO=∠BCO=60°,所以∠AOB=∠ACB=120°,然后讨论:当点P在优弧AB上,则∠APB=$\frac{1}{2}$∠AOB=60°;当点P在劣弧AB上,则∠APB=∠ACB=120°.
解答 解: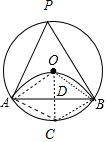 作OD⊥AB于D,交⊙O于C,连接OA、OB、AC、BC,如图,
作OD⊥AB于D,交⊙O于C,连接OA、OB、AC、BC,如图,
∵⊙O沿弦AB折叠,圆弧恰好经过圆心O,
∴AB垂直平分OC,
∴OC垂直平分AB,
∴四边形ACBO为菱形,
∴OA=OB=AC=BC,
∴△AOC和△BOC都是等边三角形,
∴∠AOC=∠BOC=∠ACO=∠BCO=60°,
∴∠AOB=∠ACB=120°,
当点P在优弧AB上,则∠APB=$\frac{1}{2}$∠AOB=60°;
当点P在劣弧AB上,则∠APB=∠ACB=120°.
故答案为60°或120.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理.

练习册系列答案
相关题目
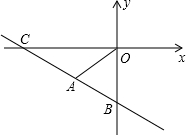 如图,一次函数y=ax-b与正比例函数y=kx的图象交于第三象限内的点A,与y轴交于B(0,-4),且OA=AB,△AOB的面积为6.
如图,一次函数y=ax-b与正比例函数y=kx的图象交于第三象限内的点A,与y轴交于B(0,-4),且OA=AB,△AOB的面积为6. 如图所示,一根木棒AB长为2,斜靠在与地面OM垂直的墙壁ON上,与地面的倾斜角(∠ABO)为60°,当木棒A端沿NO向下滑动到A′,B端沿直线OM向右滑动到B′,若AA′=$\sqrt{3}$-1,则木棒的中点从P随之运动到P′所经过的路径长为$\frac{π}{6}$.
如图所示,一根木棒AB长为2,斜靠在与地面OM垂直的墙壁ON上,与地面的倾斜角(∠ABO)为60°,当木棒A端沿NO向下滑动到A′,B端沿直线OM向右滑动到B′,若AA′=$\sqrt{3}$-1,则木棒的中点从P随之运动到P′所经过的路径长为$\frac{π}{6}$.