题目内容
1．
如图，在菱形ABCD中，对角线AC、BD相交于O点，E是AD的中点，连接OE，若OE=2，则菱形ABCD的周长等于16．
分析 由菱形的性质可得出AC⊥BD，AB=BC=CD=DA，再根据直角三角形斜边上的中线等于斜边的一半得出AD的长，结合菱形的周长公式即可得出结论．
解答 解：∵四边形ABCD为菱形，
∴AC⊥BD，AB=BC=CD=DA，
∴△AOD为直角三角形．
∵OE=2，且点E为线段AD的中点，
∴AD=2OE=4．
C菱形ABCD=4AD=4×4=16．
故答案为16
点评 本题考查了菱形的性质以及直角三角形的性质，解题的关键是求出AD=4．本题属于基础题，难度不大．
练习册系列答案
相关题目
11．有五张卡片（形状、大小、质地都相同），正面分别画有下列图形：①线段；②正三角形；③平行四边形；④圆；⑤菱形．将卡片背面朝上洗匀，从中抽取一张，其正面图形既是轴对称图形，又是中心对称图形的概率是（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
9．若把分式$\frac{xy}{3x-y}$中的x和y都扩大2倍，那么分式的值（ ）
| A． | 扩大2倍 | B． | 不变 | C． | 缩小2倍 | D． | 缩小4倍 |
16．一元二次方程4x2-12x+9=0的根的情况是（ ）
| A． | 有两个不相等的实数根 | B． | 有两个相等的实数根 | ||
| C． | 无实数根 | D． | 无法确定 |
6．
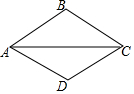在菱形ABCD中，∠BAD=60°，则边AB=4，对角线AC长为（ ）
在菱形ABCD中，∠BAD=60°，则边AB=4，对角线AC长为（ ）| A． | 4 | B． | 2$\sqrt{3}$ | C． | 4$\sqrt{3}$ | D． | 2 |
13．
如图，在菱形ABCD中，AB=4，AD边的垂直平分线交AC于点N，△CND的周长是10，则AC的长为（ ）
如图，在菱形ABCD中，AB=4，AD边的垂直平分线交AC于点N，△CND的周长是10，则AC的长为（ ）| A． | 6 | B． | 8 | C． | 10 | D． | 12 |
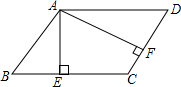已知?ABCD中，AB=4，BC=6，BC边上的高AE=3，则DC边上的高AF的长是4.5．