Question

【题目】如图，在平面直角坐标系中，点P的坐标为(－4，0)，⊙P的半径为2，将⊙P沿x轴向右平移4个单位得到⊙P1.

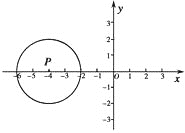
(1)画出⊙P1 ， 并直接判断⊙P与⊙P1的位置关系．

(2)设⊙P1与x轴正半轴，y轴正半轴的交点分别为A、B，求劣弧AB与弦AB围成的图形的面积．(结果保留π)

Answer 1

【答案】（1）图见解析，与⊙P的位置关系为外切；（2）π－2

【解析】

（1）根据题意作图即可求得答案，注意圆的半径为2；
（2）首先根据题意求得扇形BP1A与△BP1A的面积，再作差即可求得劣弧与弦AB围成的图形的面积．

解：(1)⊙P1的位置如图所示，它与⊙P的位置关系为外切．

(2)S扇形OAB＝π×22＝π，

S△AOB＝×2×2＝2.

∴劣弧AB与弦AB围成的图形的面积为：π－2.