题目内容
10.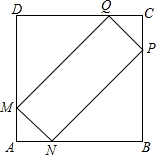 已知:如图,在边长为6cm的正方形ABCD中,动点M、N从点A分别沿边AD、AB运动至点D、B停止,动点P、Q从点C分别沿边CB、CD运动至点B、D停止,它们同时出发,设动点速度均为1cm/s,运动时间为t s,连接MN、NP、PQ、QM.
已知:如图,在边长为6cm的正方形ABCD中,动点M、N从点A分别沿边AD、AB运动至点D、B停止,动点P、Q从点C分别沿边CB、CD运动至点B、D停止,它们同时出发,设动点速度均为1cm/s,运动时间为t s,连接MN、NP、PQ、QM.(1)试说明在运动过程中,四边形MNPQ是矩形;
(2)在运动过程中,当t为何值时,四边形MNPQ是正方形?
(3)在运动过程中,当t为何值时,△PNB沿折痕PN翻折得到△PNB′,使得 点B′恰好落在MQ上?
(4)将△MNA、△PNB、△PQC、△MQD同时沿折痕MN、PN、QP、MQ翻折,得△MNA′、△PNB′△PQC′、△MQD′,若其中两个三角形重叠部分的面积为4cm2,请直接写出动点运动时间t的值.
分析 (1)首先证明△QCP≌△MAN、△AMN≌△CQP,从而得到MN=QP,MQ=NP,然后再证明∠MQP=90°;
(2)由正方形的性质可知:MQ=QP,然后证明△DQM≌△CQP,从而得到QC=DQ=3;
(3)如图1所示,首先证明四边形B′NBP为正方形从而得到NM=OB′=OB.,然后由勾股定理求得,MN、PB的长,然后由BC=CP+PB,列方程求解即可;
(4)如图2所示;根据题意可知:四边形QCPC′、四边形B′A′D′C′、四边形MANA′均为正方形,最后根据AM+B′A′+CP=6,列方程求解即可;如图3所示:根据DM+D′C′+PB=6列方程求解.
解答 证明:(1)∵动点速度均为1cm/s,
∴QC=CP=AM=AN.
∵ABCD为正方形,
∴AB=BC=CD=AD.
∴QO=MD=BN=BP.
在△QCP和△MAN中$\left\{\begin{array}{l}{QC=AM}\\{∠C=∠A}\\{PC=AN}\end{array}\right.$,
∴△QCP≌△MAN.
∴MN=QP.
同理:MQ=NP.
∴四边形MNPQ为平行四边形.
∵∠C=90°,QC=CP,
∴∠CQP=45°.
同理:∠DQM=45°.
∴∠MQP=90°.
∴四边形MNPQ为矩形.
(2)∵四边形MNPQ为正方形,
∴MQ=QP.
∵∠CQP=45°,∠DQM=45°,
∴∠CQP=∠DQM.
在△DQM和△CQP中$\left\{\begin{array}{l}{∠C=∠D}\\{∠CQP=∠DQM}\\{QP=QM}\end{array}\right.$,
∴△DQM≌△CQP.
∴QC=DQ=3.
∴t=3s.
(3)如图1所示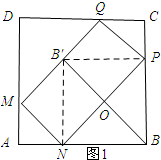
∵△PBN为等腰直角三角形,
由折叠的性质可知四边形B′NBP为正方形.
∴NM=OB′=OB.
在△MNA中,$MN=\sqrt{A{M}^{2}+A{N}^{2}}=\sqrt{2}t$,在△POB中,PB=$\sqrt{O{P}^{2}+O{B}^{2}}=2t$.
∵BC=CP+PB,
∴t+2t=6.
∴t=2s.
(4)如图2所示;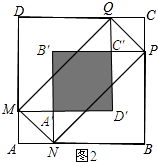
∵△MNA、△BNP、△QCP、△DQM均为等腰直角三角形,
由翻折的性质可知:四边形QCPC′、四边形B′A′D′C′、四边形MANA′均为正方形.
∵重叠部分的面积为4,
∴B′A′=2.
∵AM+B′A′+CP=6.
∴2t+2=6.
∴t=2s.
如图3所示:DM+D′C′+PB=6.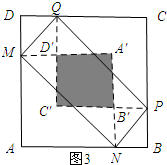
∴(6-t)+2+(6-t)=6.
解得:t=4.
综上所述,当t=2s或4s时,重合部分的面积为4cm2.
点评 本题主要考查的翻折的性质、等腰直角三角形的性质、矩形的判定、全等三角形的性质和判定,根据题意画出符合题意的图形是解题的关键.

| A. | $\left\{\begin{array}{l}{8x+6y=30}\\{x+y=200}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{6x+8y=30}\\{x+y=200}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=30}\\{8x+6y=200}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=30}\\{6x+8y=200}\end{array}\right.$ |
| A. | -(-$\frac{1}{2}$) | B. | (-$\frac{1}{2}$)2 | C. | (-2)3 | D. | (-2)0 |