题目内容
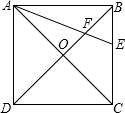 如图:AE是正方形ABCD中∠BAC的平分线,AE分别交BD、BC于F、E,AC、BD相交于O,
如图:AE是正方形ABCD中∠BAC的平分线,AE分别交BD、BC于F、E,AC、BD相交于O,(1)求证:BE=BF;
(2)求证:OF=
| 1 |
| 2 |
考点:正方形的性质,等腰三角形的判定与性质,三角形中位线定理
专题:证明题
分析:(1)根据正方形的性质可求得∠ABE=∠AOF=90°,由于AE是正方形ABCD中∠BAC的平分线,根据等角的余角相等即可求得∠AFO=∠AEB,根据对顶角相等即可求得∠BFE=∠AEB,根据等角对等边即可证得BE=BF;
(2)连接O和AE的中点G,根据三角形的中位线的性质即可证得OG∥BC,OG=
CE,根据平行线的性质即可求得∠OGF=∠FEB,从而证得∠OGF=∠AFO,根据等角对等边即可证得OG=OF,进而证得OF=
CE.
(2)连接O和AE的中点G,根据三角形的中位线的性质即可证得OG∥BC,OG=
| 1 |
| 2 |
| 1 |
| 2 |
解答:(1)证明:∵四边形ABCD是正方形,
∴AC⊥BD,
∴∠ABE=∠AOF=90°,
∵∠CAE=∠BAE,
∴∠AFO=∠AEB,
∴∠BFE=∠AEB,
∴BE=BF.
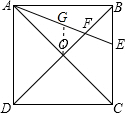 (2)证明:连接O和AE的中点G,
(2)证明:连接O和AE的中点G,
∵AO=CO,AG=EG,
∴OG∥BC,OG=
CE,
∴∠OGF=∠FEB,
∵∠AFO=∠AEB,
∴∠OGF=∠AFO,
∴OG=OF,
∴OF=
CE.
∴AC⊥BD,
∴∠ABE=∠AOF=90°,
∵∠CAE=∠BAE,
∴∠AFO=∠AEB,
∴∠BFE=∠AEB,
∴BE=BF.
 (2)证明:连接O和AE的中点G,
(2)证明:连接O和AE的中点G,∵AO=CO,AG=EG,
∴OG∥BC,OG=
| 1 |
| 2 |
∴∠OGF=∠FEB,
∵∠AFO=∠AEB,
∴∠OGF=∠AFO,
∴OG=OF,
∴OF=
| 1 |
| 2 |
点评:本题考查了正方形的性质,等腰三角形的判定,三角形的中位线定理等,熟练掌握性质和定理是解题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
一个长方形的长与宽分别时6cm、5cm,它的对角线的长可能是( )
| A、整数 | B、分数 |
| C、有理数 | D、无理数 |
 已知:如图,在△ABC中,∠ABC与∠ACB的平分线相交于点O.
已知:如图,在△ABC中,∠ABC与∠ACB的平分线相交于点O. 如图,直线a上有5个点,A1,A2,…,A5,图中共有多少个三角形?
如图,直线a上有5个点,A1,A2,…,A5,图中共有多少个三角形? 已知:如图AD•AB=AF•AC,求证:△DEB∽△FEC.
已知:如图AD•AB=AF•AC,求证:△DEB∽△FEC. 某校针对某事件在本校学生中做了一次抽样调查,并把调查结果分为三种类型:
某校针对某事件在本校学生中做了一次抽样调查,并把调查结果分为三种类型: