题目内容
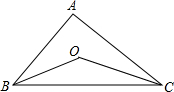 已知:如图,在△ABC中,∠ABC与∠ACB的平分线相交于点O.
已知:如图,在△ABC中,∠ABC与∠ACB的平分线相交于点O.求证:∠BOC=90°+
| 1 |
| 2 |
考点:三角形内角和定理
专题:证明题
分析:根据角平分线的定义可得∠OBC=
∠ABC,∠OCB=
∠ACB,然后表示出∠OBC+∠OCB,再根据三角形的内角和等于180°列式整理即可得证.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:∵∠ABC与∠ACB的平分线相交于点O,
∴∠OBC=
∠ABC,∠OCB=
∠ACB,
∴∠OBC+∠OCB=
(∠ABC+∠ACB),
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)
=180°-
(∠ABC+∠ACB)
=180°-
(180°-∠A)
=90°+
∠A,
即:∠BOC=90°+
∠A.
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OBC+∠OCB=
| 1 |
| 2 |
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)
=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
即:∠BOC=90°+
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
点P(-2,-4)与点Q(6,-4)的位置关系是( )
| A、关于x轴对称 |
| B、关于y轴对称 |
| C、关于直线x=2对称 |
| D、关于直线y=2对称 |
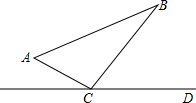 如图,△ABC中,∠ACB=90°,AC=6BC=8.点P从点出发沿A-C-B路径向终点运动,终点为B点;点Q从B点出发沿B-C-A路径向终点运动,终点为A点.点P和Q分别以1和3的运动速度同时开始运动,一点到相应的终点停止运动,某时刻,分别过P和Q作PE⊥L于E,QF⊥L于F.问:点P运动多少时间时,△PEC与QFC全等?请说明理由.
如图,△ABC中,∠ACB=90°,AC=6BC=8.点P从点出发沿A-C-B路径向终点运动,终点为B点;点Q从B点出发沿B-C-A路径向终点运动,终点为A点.点P和Q分别以1和3的运动速度同时开始运动,一点到相应的终点停止运动,某时刻,分别过P和Q作PE⊥L于E,QF⊥L于F.问:点P运动多少时间时,△PEC与QFC全等?请说明理由.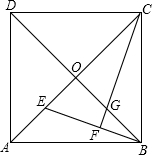 如图,已知正方形ABCD的对角线AC、BD相交于点O,BE平分∠OBA,CF⊥BE于F,交OB于G.
如图,已知正方形ABCD的对角线AC、BD相交于点O,BE平分∠OBA,CF⊥BE于F,交OB于G.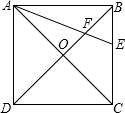 如图:AE是正方形ABCD中∠BAC的平分线,AE分别交BD、BC于F、E,AC、BD相交于O,
如图:AE是正方形ABCD中∠BAC的平分线,AE分别交BD、BC于F、E,AC、BD相交于O,