题目内容
 如图,已知,AC是⊙O的直径,B是圆上一点,连接AB、OB、CB,若∠A=30°,AB=3cm,则图中阴影部分的面积为________cm2(结果保留π).
如图,已知,AC是⊙O的直径,B是圆上一点,连接AB、OB、CB,若∠A=30°,AB=3cm,则图中阴影部分的面积为________cm2(结果保留π).
π
分析:首先,在Rt△ABC中利用三角函数的定义求得直径AC的长度,则易求半径OA的长度;
其次,利用圆周角定理求得∠COB=60°,在易求∠AOB=120°;
最后,由扇形面积公式求得图中阴影部分的面积.
解答:如图,∵AC是直径,
∴∠ABC=90°.
∴在Rt△ABC中,∠A=30°,AB=3cm,则AC= =2
=2 cm,
cm,
∴OA=OB= AC=
AC= cm.
cm.
又∠COB=2∠A=60°,
∴∠AOB=120°,
∴图中阴影部分的面积为: =π(cm2).
=π(cm2).
故答案是:π.
点评:本题考查了扇形面积的计算,解答时,要熟记扇形面积公式S= .
.
分析:首先,在Rt△ABC中利用三角函数的定义求得直径AC的长度,则易求半径OA的长度;
其次,利用圆周角定理求得∠COB=60°,在易求∠AOB=120°;
最后,由扇形面积公式求得图中阴影部分的面积.
解答:如图,∵AC是直径,
∴∠ABC=90°.
∴在Rt△ABC中,∠A=30°,AB=3cm,则AC=
 =2
=2 cm,
cm,∴OA=OB=
 AC=
AC= cm.
cm.又∠COB=2∠A=60°,
∴∠AOB=120°,
∴图中阴影部分的面积为:
 =π(cm2).
=π(cm2).故答案是:π.
点评:本题考查了扇形面积的计算,解答时,要熟记扇形面积公式S=
 .
. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
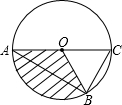 (2013•雨花台区一模)如图,已知,AC是⊙O的直径,B是圆上一点,连接AB、OB、CB,若∠A=30°,AB=3cm,则图中阴影部分的面积为
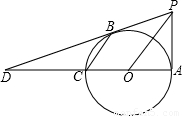
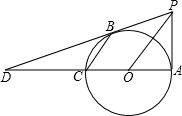
(2013•雨花台区一模)如图,已知,AC是⊙O的直径,B是圆上一点,连接AB、OB、CB,若∠A=30°,AB=3cm,则图中阴影部分的面积为 如图,已知:AC是⊙O的直径,PA⊥AC,连接OP,弦CB∥OP,直线PB交直线AC于D,BD=2PA.
如图,已知:AC是⊙O的直径,PA⊥AC,连接OP,弦CB∥OP,直线PB交直线AC于D,BD=2PA.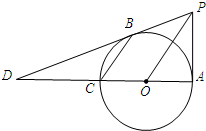 如图,已知:AC是⊙O的直径,PA⊥AC,连接OP,弦CB∥OP,直线PB交直线AC于D,BD=2PA.
如图,已知:AC是⊙O的直径,PA⊥AC,连接OP,弦CB∥OP,直线PB交直线AC于D,BD=2PA.