题目内容
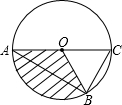（2013•雨花台区一模）如图，已知，AC是⊙O的直径，B是圆上一点，连接AB、OB、CB，若∠A=30°，AB=3cm，则图中阴影部分的面积为π
π
cm2（结果保留π）．分析：首先，在Rt△ABC中利用三角函数的定义求得直径AC的长度，则易求半径OA的长度；
其次，利用圆周角定理求得∠COB=60°，在易求∠AOB=120°；
最后，由扇形面积公式求得图中阴影部分的面积．
其次，利用圆周角定理求得∠COB=60°，在易求∠AOB=120°；
最后，由扇形面积公式求得图中阴影部分的面积．
解答：解：如图，∵AC是直径，
∴∠ABC=90°．
∴在Rt△ABC中，∠A=30°，AB=3cm，则AC=
=2
cm，
∴OA=OB=
AC=
cm．
又∠COB=2∠A=60°，
∴∠AOB=120°，
∴图中阴影部分的面积为：
=π（cm2）．
故答案是：π．
∴∠ABC=90°．
∴在Rt△ABC中，∠A=30°，AB=3cm，则AC=
| AB |
| cos30° |
| 3 |
∴OA=OB=
| 1 |
| 2 |
| 3 |
又∠COB=2∠A=60°，
∴∠AOB=120°，
∴图中阴影部分的面积为：
120π×(
| ||
| 360 |
故答案是：π．
点评：本题考查了扇形面积的计算，解答时，要熟记扇形面积公式S=
．
| nπR2 |
| 360 |
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
（2013•雨花台区一模）如图，在8×4的矩形网格中，每格小正方形的边长都是1，若△ABC的三个顶点在图中相应的格点上，则sin∠BAC的值为（ ）
（2013•雨花台区一模）如图，矩形ABCD中，AB=3，BC=5，点P是BC边上的一个动点（点P不与点B、C重合），现将△PCD沿直线PD折叠，使点C落到点C′处；作∠BPC′的角平分线交AB于点E．设BP=x，BE=y，则下列图象中，能表示y与x的函数关系的图象大致是（ ）