题目内容
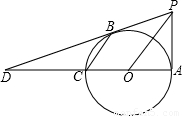
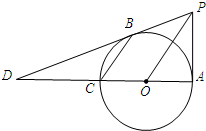 如图,已知:AC是⊙O的直径,PA⊥AC,连接OP,弦CB∥OP,直线PB交直线AC于D,BD=2PA.
如图,已知:AC是⊙O的直径,PA⊥AC,连接OP,弦CB∥OP,直线PB交直线AC于D,BD=2PA.
(1)证明:直线PB是⊙O的切线;
(2)探究线段PO与线段BC之间的数量关系,并加以证明.
 (1)证明:连接OB.
(1)证明:连接OB.∵BC∥OP,
∴∠BCO=∠POA,∠CBO=∠POB.
又∵OC=OB,
∴∠BCO=∠CBO,
∴∠POB=∠POA.
又∵PO=PO,OB=OA,
∴△POB≌△POA,
∴∠PBO=∠PAO=90°,
∴PB是⊙O的切线
(2)2PO=3BC(写
 亦可).
亦可).证明:∵△POB≌△POA,
∴PB=PA.
∵BD=2PA,
∴BD=2PB.
∵BC∥PO,
∴△DBC∽△DPO.
∴
 (相似三角形的对应边成比例),
(相似三角形的对应边成比例),∴2PO=3BC.
注:开始没有写出判断结论,证明正确也给满分、
分析:(1)连接OB.欲证明直线PB是⊙O的切线,只需证明OB⊥PB即可;
(2)根据(1)中全等三角形(△POB≌△POA)的对应边相等推知PB=PA,由已知条件“BD=2PA”、等量代换可以求得BD=2PB;然后由相似三角形(△DBC∽△DPO)的对应边成比例可以求得
 ,从而解得2PO=3BC.
,从而解得2PO=3BC.点评:本题考查了切线的判定与性质.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
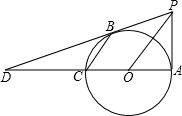
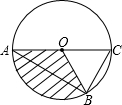 (2013•雨花台区一模)如图,已知,AC是⊙O的直径,B是圆上一点,连接AB、OB、CB,若∠A=30°,AB=3cm,则图中阴影部分的面积为
(2013•雨花台区一模)如图,已知,AC是⊙O的直径,B是圆上一点,连接AB、OB、CB,若∠A=30°,AB=3cm,则图中阴影部分的面积为 如图,已知:AC是⊙O的直径,PA⊥AC,连接OP,弦CB∥OP,直线PB交直线AC于D,BD=2PA.
如图,已知:AC是⊙O的直径,PA⊥AC,连接OP,弦CB∥OP,直线PB交直线AC于D,BD=2PA.