题目内容
11. 如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{6}$ | C. | 3 | D. | $\sqrt{6}$ |
分析 由于点B与D关于AC对称,所以连接BD,与AC的交点即为F点.此时PD+PE=BE最小,而BE是等边△ABE的边,BE=AB,由正方形ABCD的面积为12,可求出AB的长,从而得出结果.
解答 解:连接BD,与AC交于点F.
∵点B与D关于AC对称,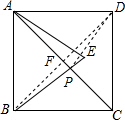
∴PD=PB,
∴PD+PE=PB+PE=BE最小.
∵正方形ABCD的面积为12,
∴AB=2$\sqrt{3}$.
又∵△ABE是等边三角形,
∴BE=AB=2$\sqrt{3}$.
故所求最小值为2$\sqrt{3}$.
故选A.
点评 此题主要考查轴对称-最短路线问题、正方形的性质等知识,解题的关键是学会利用对称解决最短问题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
1.下列不等式中是一元一次不等式的是( )
| A. | $\frac{1}{2}$x-y<1 | B. | x2+5x-1≥0 | C. | x+y2>3 | D. | 2x<4-3x |
2.已知$\sqrt{2a+\sqrt{4a-1}}$+$\sqrt{2a-\sqrt{4a-1}}$=$\sqrt{2}$成立,则a的取值范围是( )
| A. | $\frac{1}{4}$≤a≤$\frac{1}{2}$ | B. | $\frac{1}{4}$<a<$\frac{1}{2}$ | C. | $\frac{1}{3}$≤a≤$\frac{1}{2}$ | D. | $\frac{1}{2}$≤a≤1 |
6.已知,点P(1-t,t+2)随着t的变化,点P不可能在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.下列命题中是假命题的是( )
| A. | 若a>b,则2a>2b | B. | 若-2a<-2b,则a>b | ||
| C. | 若a-1<b-1,则a>b | D. | 若a>b,则-a-1<-b-1 |
3.(2017,石家庄裕华区模拟)在学习三角形中位线的性质时,小亮对课本给出的解决办法进行了认真思考:

请你利用小亮的发现解决下列问题:
(1)如图③,AD是△ABC的中线,BE交AC于点E,交AD于点F,且AE=EF,求证:AC=BF.

请你帮助小亮写出辅助线作法并完成论证过程:
(2)解决问题:如图⑤,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线.过点D,E作DF∥EG,分别交BC于点F,G,过点A作MN∥BC,分别与FD,GE的延长线交于点M,N,则四边形MFGN周长的最小值是8+10$\sqrt{2}$.
| 课本研究三角形中位线性质的方法 已知:如图①,已知△ABC中,D,E分别是AB,AC两边中点.求证:DE∥BC,DE=$\frac{1}{2}$BC. 证明:延长DE至点F,使EF=DE,连接FC.…则△ADE≌△CFE.∴…  |

请你利用小亮的发现解决下列问题:
(1)如图③,AD是△ABC的中线,BE交AC于点E,交AD于点F,且AE=EF,求证:AC=BF.

请你帮助小亮写出辅助线作法并完成论证过程:
(2)解决问题:如图⑤,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线.过点D,E作DF∥EG,分别交BC于点F,G,过点A作MN∥BC,分别与FD,GE的延长线交于点M,N,则四边形MFGN周长的最小值是8+10$\sqrt{2}$.
1. 如图是王老师去公园锻炼及原路返回时离家的距离y(千米)与时间t(分钟)之间的函数图象,根据图象信息,下列说法正确的是( )
如图是王老师去公园锻炼及原路返回时离家的距离y(千米)与时间t(分钟)之间的函数图象,根据图象信息,下列说法正确的是( )
 如图是王老师去公园锻炼及原路返回时离家的距离y(千米)与时间t(分钟)之间的函数图象,根据图象信息,下列说法正确的是( )
如图是王老师去公园锻炼及原路返回时离家的距离y(千米)与时间t(分钟)之间的函数图象,根据图象信息,下列说法正确的是( )| A. | 王老师去时所用的时间少于回家的时间 | |
| B. | 王老师去公园锻炼了40分钟 | |
| C. | 王老师去时走上坡路,回家时走下坡路 | |
| D. | 王老师去时速度比回家时速度慢 |