题目内容
6.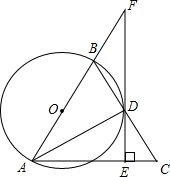 如图,以△ABC的边AB为直径的⊙O与边BC交于点D,过点D作DE⊥AC,垂足为E,延长AB、ED交于点F,AD平分∠BAC.
如图,以△ABC的边AB为直径的⊙O与边BC交于点D,过点D作DE⊥AC,垂足为E,延长AB、ED交于点F,AD平分∠BAC.(1)求证:EF是⊙O的切线;
(2)若CE=1,sinF=$\frac{3}{5}$,求⊙O的半径.
分析 (1)连接OD,根据OA=OD和角平分线性质得出∠ODA=∠DAE,推出OD∥AC,得出∠ODE=90°,根据切线的判定推出即可;
(2)根据平行线得出BD=CD,根据切线的性质得出∠BDF=∠BAD,进而得出∠EDC=∠CAD,即可得出AD⊥DB,根据垂直平分线的性质求得AB=AC,从而列出$\frac{8}{5}$x+1=2x,求出即可.
解答 解:(1)连接OD,
∵AD平分∠BAC,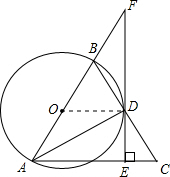
∴∠FAD=∠DAE,
又∵∠OAD=∠ODA,
∴∠ODA=∠DAE,
∴OD∥AE,
∵DE⊥AC,
∴EF⊥OD,
∴EF是⊙O的切线;
(2)解:设⊙O的半径为x.
∵OD∥AE,OA=OB,
∴BD=CD,
∵EF是⊙O的切线;
∴∠BDF=∠BAD,
∵∠BAD=∠CAD,∠BDF=∠EDC,
∴∠EDC=∠CAD,
∵DE⊥AC,
∴∠EDC+∠C=90°,
∴∠CAD+∠C=90°,
∴∠ADC=90°,
∴AD⊥DB,
∴AC=AB,
∵sinF=$\frac{3}{5}$,
∴OF=$\frac{5}{3}$OD=$\frac{5}{3}$x,
∴BF=$\frac{5}{3}$x-x=$\frac{2}{3}$x,AF=$\frac{2}{3}$x+2x=$\frac{8}{3}$x,
∴AE=$\frac{3}{5}$AF=$\frac{3}{5}$×$\frac{8}{3}$x=$\frac{8}{5}$x,
∵AC=AB,
∴AE+EC=2x,
即$\frac{8}{5}$x+1=2x,
解得:x=$\frac{5}{2}$.
∴⊙O的半径为$\frac{5}{2}$.
点评 本题考查了切线的判定、解直角三角形、角平分线性质、平行线的性质和判定,解(1)的关键是求出∠ODE=90°,解(2)的关键是得出关于x的方程.

 阅读快车系列答案
阅读快车系列答案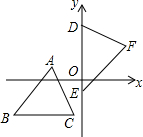 如图,坐标平面上,△ABC≌△DEF,其中A、B、C的对应顶点分别为D,E,F,且AB=BC=5.若A点的坐标为(-3,1),B、C两点的纵坐标都是-3,D、E两点在y轴上,则点F到y轴的距离为( )
如图,坐标平面上,△ABC≌△DEF,其中A、B、C的对应顶点分别为D,E,F,且AB=BC=5.若A点的坐标为(-3,1),B、C两点的纵坐标都是-3,D、E两点在y轴上,则点F到y轴的距离为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 1800 |
| 第二周 | 4台 | 10台 | 3100 |
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5730元的金额再采购这两种型号的电风扇共30台,在全部售完30台电风扇情况下,使利润不少于1400元,请你帮助超市分析有哪几种采购方案?
 如图,EF∥BC,AC平分∠BAF,∠B=50°,则∠C的度数是( )
如图,EF∥BC,AC平分∠BAF,∠B=50°,则∠C的度数是( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
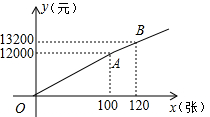 为了发展本地足球运动,在体育局的策划下,市体育馆将举行明星足球邀请赛,为此体育局推出两种购票方案(设购票张数为x,购票总价为y):方案一:提供8 000元赞助后,每张票的票价为50元,方案二:票价按下图中的折线OAB所表示的函数关系确定.
为了发展本地足球运动,在体育局的策划下,市体育馆将举行明星足球邀请赛,为此体育局推出两种购票方案(设购票张数为x,购票总价为y):方案一:提供8 000元赞助后,每张票的票价为50元,方案二:票价按下图中的折线OAB所表示的函数关系确定.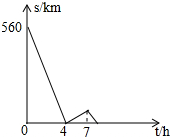 一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后分别按原速同时驶往甲地,两车之间的距离S(km)与慢车行驶时间t(h)之间的函数图象如图所示,下列说法:
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后分别按原速同时驶往甲地,两车之间的距离S(km)与慢车行驶时间t(h)之间的函数图象如图所示,下列说法: