题目内容
17.某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 1800 |
| 第二周 | 4台 | 10台 | 3100 |
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5730元的金额再采购这两种型号的电风扇共30台,在全部售完30台电风扇情况下,使利润不少于1400元,请你帮助超市分析有哪几种采购方案?
分析 (1)设A、B两种型号电风扇的销售单价分别为x元、y元,根据3台A型号5台B型号的电扇收入1800元,4台A型号10台B型号的电扇收入3100元,列方程组求解;
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(30-a)台,根据金额不多于5730元,使利润不少于1400元,列不等式组求解.
解答 解:(1)设A、B两种型号电风扇的销售单价分别为x元、y元,
依题意得:$\left\{\begin{array}{l}{3x+5y=1800}\\{4x+10y=3100}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=250}\\{y=210}\end{array}\right.$.
答:A、B两种型号电风扇的销售单价分别为250元、210元;
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(30-a)台.
依题意得:$\left\{\begin{array}{l}{200a+170(30-a)≤5730}\\{(250-200)a+(210-170)(30-a)≥1400}\end{array}\right.$,
解得:20≤a≤21.
∵a是正整数,
∴a=20或a=21,
30-a=10或30-a=9.
∴共有两种方案:①采购A型20台,B型10台;②采购A型21台,B型9台.
点评 本题考查了二元一次方程组和一元一次不等式的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系和不等关系,列方程组和不等式求解.

练习册系列答案
相关题目
7.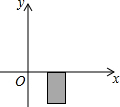 在一次科学探测活动中,探测人员发现一目标在如图所示的阴影区域内,则目标的坐标可能是( )
在一次科学探测活动中,探测人员发现一目标在如图所示的阴影区域内,则目标的坐标可能是( )
 在一次科学探测活动中,探测人员发现一目标在如图所示的阴影区域内,则目标的坐标可能是( )
在一次科学探测活动中,探测人员发现一目标在如图所示的阴影区域内,则目标的坐标可能是( )| A. | (-3,300) | B. | (7,-500) | C. | (9,600) | D. | (-2,-800) |
12.已知点P(a,b)在x轴的下方y轴的右侧,那么点P到x轴的距离是( )
| A. | a | B. | b | C. | -a | D. | -b |
2.小明在利用完全平方公式计算一个二项整式的平方时,不小心用墨水把中间一项的系数染黑了,得到正确的结果为4a2■ab+9b2,则中间一项的系数是( )
| A. | 12 | B. | -12 | C. | 12或-12 | D. | 36 |
9.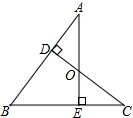 如图,AE与CD相交于点O,∠ADO=∠CEO=90°,下列条件中,不能证明△AOD≌△COE的是( )
如图,AE与CD相交于点O,∠ADO=∠CEO=90°,下列条件中,不能证明△AOD≌△COE的是( )
 如图,AE与CD相交于点O,∠ADO=∠CEO=90°,下列条件中,不能证明△AOD≌△COE的是( )
如图,AE与CD相交于点O,∠ADO=∠CEO=90°,下列条件中,不能证明△AOD≌△COE的是( )| A. | AO=CO | B. | DO=EO | C. | AD=CE | D. | ∠A=∠C |




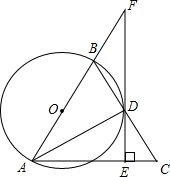 如图,以△ABC的边AB为直径的⊙O与边BC交于点D,过点D作DE⊥AC,垂足为E,延长AB、ED交于点F,AD平分∠BAC.
如图,以△ABC的边AB为直径的⊙O与边BC交于点D,过点D作DE⊥AC,垂足为E,延长AB、ED交于点F,AD平分∠BAC.