题目内容
6.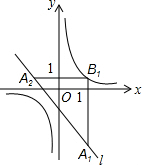 如图,在平面直角坐标系中,已知直线l:y=-x-1,双曲线y=$\frac{1}{x}$,在直线l上取点A1,过点A1作x轴的垂线交双曲线于点B1,过点B1作y轴的垂线交直线l于点A2,过点A2作x轴的垂线交双曲线于点B2,过点B2作y轴的垂线交直线l于点A3…,这样依次得到直线l上的点A1,A2,A3,A4,…,An,…若点A1的横坐标为2,则点A2015的坐标为(-$\frac{3}{2}$,$\frac{1}{2}$).
如图,在平面直角坐标系中,已知直线l:y=-x-1,双曲线y=$\frac{1}{x}$,在直线l上取点A1,过点A1作x轴的垂线交双曲线于点B1,过点B1作y轴的垂线交直线l于点A2,过点A2作x轴的垂线交双曲线于点B2,过点B2作y轴的垂线交直线l于点A3…,这样依次得到直线l上的点A1,A2,A3,A4,…,An,…若点A1的横坐标为2,则点A2015的坐标为(-$\frac{3}{2}$,$\frac{1}{2}$).
分析 先利用一次函数图象上点的坐标特征得到A1(2,-3),由A1B1⊥x轴得到B1点的横坐标为2,则利用反比例函数图象上点的坐标特征得到B1(2,$\frac{1}{2}$),同理依次得到A2(-$\frac{3}{2}$,$\frac{1}{2}$),B2(-$\frac{2}{3}$,-$\frac{2}{3}$),A3(-$\frac{1}{3}$,-$\frac{2}{3}$),B3(-$\frac{1}{3}$,-3),A4(2,-3),则可发现点A1与点A4的坐标相同,而2015=3×671+2,于是利用规律得到点A2015的坐标为与点A2的坐标相同,即A2015(-$\frac{3}{2}$,$\frac{1}{2}$).
解答 解:当x=2时,y=-x-1=-3,则A1(2,-3),
∵A1B1⊥x轴,
∴B1点的横坐标为2,
当x=2时,y=$\frac{1}{x}$=$\frac{1}{2}$,则B1(2,$\frac{1}{2}$),
同理,当y=$\frac{1}{2}$时,-x-1=$\frac{1}{2}$,解得x=-$\frac{3}{2}$,则A2(-$\frac{3}{2}$,$\frac{1}{2}$),
当x=-$\frac{3}{2}$时,y=$\frac{1}{x}$=-$\frac{2}{3}$,则B2(-$\frac{2}{3}$,-$\frac{2}{3}$),
当y=-$\frac{2}{3}$时,-x-1=-$\frac{2}{3}$,解得x=-$\frac{1}{3}$则A3(-$\frac{1}{3}$,-$\frac{2}{3}$),
当x=-$\frac{1}{3}$时,y=$\frac{1}{x}$=-3,则B3(-$\frac{1}{3}$,-3),
当y=-3时,-x-1=-3,解得x=2,则A4(2,-3),
而2015=3×671+2,
∴点A2015的坐标为与点A2的坐标相同,
即A2015(-$\frac{3}{2}$,$\frac{1}{2}$).
故答案为(-$\frac{3}{2}$,$\frac{1}{2}$).
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了一次函数图象上点的坐标特征.

 应用题作业本系列答案
应用题作业本系列答案| 图案序号n | 1 | 2 | 3 | … | n |
| 使用的灰砖块数 | 1 | 4 | … | ||
| 使用的白砖块数 | 8 | … |
(3)是否存在白砖数恰好等于灰砖数的n值,说明你的理由;
(4)若每块白砖售价为2元,每块灰砖售价为3元,每块砖的施工费用为0.5元,铺设一个图案的费用为y元,请求出y与n的函数关系式(不要求写自变量n的取值范围).

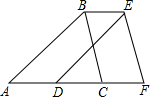 如图,将△ABC沿AC方向平移1cm得到△DEF,若△ABC的周长为10cm.则四边形ABEF的周长为( )
如图,将△ABC沿AC方向平移1cm得到△DEF,若△ABC的周长为10cm.则四边形ABEF的周长为( )| A. | 10cm | B. | 11cm | C. | 12cm | D. | 14cm |
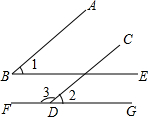 如图,已知AB∥CD,BE∥FG.
如图,已知AB∥CD,BE∥FG. 如图,已知a∥b,将三角板的直角顶点放置在直线b上,若∠1=50°,则∠2的度数为40°.
如图,已知a∥b,将三角板的直角顶点放置在直线b上,若∠1=50°,则∠2的度数为40°.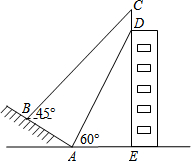 如图,山坡AB的坡度i=1:$\sqrt{3}$,AB=10米,AE=15米.在高楼的顶端竖立一块倒计时牌CD,在点B处测量计时牌的顶端C的仰角是45°,在点A处测量计时牌的底端D的仰角是60°,求这块倒计时牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,山坡AB的坡度i=1:$\sqrt{3}$,AB=10米,AE=15米.在高楼的顶端竖立一块倒计时牌CD,在点B处测量计时牌的顶端C的仰角是45°,在点A处测量计时牌的底端D的仰角是60°,求这块倒计时牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)