题目内容
19.解下列一元一次不等式(1)6x<5(x-1)+3
(2)$\frac{x+4}{2}≥\frac{x-3}{5}-4$.
分析 (1)先根据不等式的基本性质求出不等式的解集,根据不等式的解集得出答案即可;
(2)先去分母,然后通过移项、合并同类项、化系数为1进行解答.
解答 解:(1)6x<5(x-1)+3,
6x-5x<-5+3,
x<-2;
(2)$\frac{x+4}{2}≥\frac{x-3}{5}-4$,
5x+20≥2x-6-40,
3x≥-66,
x≥-22.
点评 本题考查了解简单不等式的能力,解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
9.下列各数是负数的是( )
| A. | 20 | B. | -21 | C. | $\frac{11}{7}$ | D. | 0 |
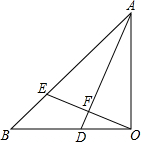 如图,△AOB中,OB=OA,∠AOB=90°,AD平分∠OAB交OB于D,OE⊥AD交AB于E,垂足为F,下列结论:
如图,△AOB中,OB=OA,∠AOB=90°,AD平分∠OAB交OB于D,OE⊥AD交AB于E,垂足为F,下列结论: