题目内容
13．
如图，分别是由若干个完全相同的小正方体组成的一个几何体的主视图和俯视图，则组成这个几何体的小正方体的个数是4或5．
分析 根据题意，主视图以及俯视图都是由3个小正方形组成，利用空间想象力可得出该几何体由4或5个小正方形组成．
解答 解：俯视图与主视图相同，可判断出底面有3个，而第二层则最少1个小正方体，最多有2个正方体．
则这个几何体的小立方块可能有4或5个．
故答案为：4或5．
点评 本题考查了由几何体的视图获得几何体的方法．在判断过程中要寻求解答的好思路，不要被几何体的各种可能情况所困绕．
练习册系列答案
相关题目
4．观察下列等式：
第一个等式：a1=$\frac{3}{1×2×{2}^{2}}$=$\frac{1}{1×2}$-$\frac{1}{2×{2}^{2}}$；
第二个等式：a2=$\frac{4}{2×3×{2}^{3}}$=$\frac{1}{2×{2}^{2}}$-$\frac{1}{3×{2}^{3}}$；
第三个等式：a3=$\frac{5}{3×4×{2}^{4}}$=$\frac{1}{3×{2}^{3}}$-$\frac{1}{4×{2}^{4}}$；
第四个等式：a4=$\frac{6}{4×5×{2}^{5}}$=$\frac{1}{4×{2}^{4}}$-$\frac{1}{5×{2}^{5}}$．
按上述规律，则式子a1+a2+a3+…+a22的结果为（ ）
第一个等式：a1=$\frac{3}{1×2×{2}^{2}}$=$\frac{1}{1×2}$-$\frac{1}{2×{2}^{2}}$；
第二个等式：a2=$\frac{4}{2×3×{2}^{3}}$=$\frac{1}{2×{2}^{2}}$-$\frac{1}{3×{2}^{3}}$；
第三个等式：a3=$\frac{5}{3×4×{2}^{4}}$=$\frac{1}{3×{2}^{3}}$-$\frac{1}{4×{2}^{4}}$；
第四个等式：a4=$\frac{6}{4×5×{2}^{5}}$=$\frac{1}{4×{2}^{4}}$-$\frac{1}{5×{2}^{5}}$．
按上述规律，则式子a1+a2+a3+…+a22的结果为（ ）
| A． | $\frac{1}{2}-\frac{1}{{21×{2^{21}}}}$ | B． | $\frac{1}{2}-\frac{1}{{22×{2^{22}}}}$ | C． | $\frac{1}{2}-\frac{1}{{23×{2^{23}}}}$ | D． | $\frac{1}{2}-\frac{1}{{24×{2^{24}}}}$ |
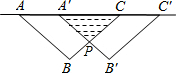如图，把等腰Rt△ABC沿AC方向平移到等腰Rt△A′B′C′的位置时，它们重叠的部分的面积是Rt△ABC面积的$\frac{1}{4}$．若AB=$\sqrt{2}$cm，则它移动的距离AA′=1cm．
4．菱形有一个内角为120°，较短对角线为6，则菱形的周长为（ ）
| A． | 12 | B． | 24 | C． | 36 | D． | 12$\sqrt{3}$ |