题目内容
1.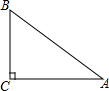 已知A,B,C三地位置如图所示,∠C=90°,A,C两地的距离是4km,B,C两地的距离是3km,则A,B两地的距离是5km;若A地在C地的正东方向,则B地在C地的正北方向.
已知A,B,C三地位置如图所示,∠C=90°,A,C两地的距离是4km,B,C两地的距离是3km,则A,B两地的距离是5km;若A地在C地的正东方向,则B地在C地的正北方向.
分析 根据勾股定理来求AB的长度.由于∠C=90°,A地在C地的正东方向,则B地在C地的正北方向.
解答  解:∵∠C=90°,A,C两地的距离是4km,B,C两地的距离是3km,
解:∵∠C=90°,A,C两地的距离是4km,B,C两地的距离是3km,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5(km).
又∵A地在C地的正东方向,则B地在C地的 正北方向.
故答案是:5;正北.
点评 本题考查了勾股定理的应用和方向角.勾股定理在实际问题中的应用:运用勾股定理的数学模型解决现实世界的实际问题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
11.化简$\frac{{a}^{2}+2ab+{b}^{2}}{{a}^{2}-{b}^{2}}$-$\frac{b}{a-b}$的结果是( )
| A. | $\frac{a}{a-b}$ | B. | $\frac{b}{a-b}$ | C. | $\frac{a}{a+b}$ | D. | $\frac{b}{a+b}$ |
12.下列运算正确的是( )
| A. | ($\frac{1}{2}$)-1=-$\frac{1}{2}$ | B. | 6×107=6000000 | C. | (2a)2=2a2 | D. | a3•a2=a5 |
16.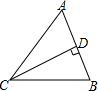 如图,△ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( )
如图,△ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( )
 如图,△ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( )
如图,△ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( )| A. | 线段CA的长 | B. | 线段CD的长 | C. | 线段AD的长 | D. | 线段AB的长 |
13.今年,我省启动了“关爱留守儿童工程”.某村小为了了解各年级留守儿童的数量,对一到六年级留守儿童数量进行了统计,得到每个年级的留守儿童人数分别为10,15,10,17,18,20.对于这组数据,下列说法错误的是( )
| A. | 平均数是15 | B. | 众数是10 | C. | 中位数是17 | D. | 方差是$\frac{44}{3}$ |