��Ŀ����
14�� ��ͼ����y����һ��P��0��1����ƽ����x���ֱ��PB���ֱ���y1=x2��x��0����y2=$\frac{{x}^{2}}{3}$��x��0����ͼ����A1��B1���㣬����B1��y���ƽ���߽�y1��ͼ���ڵ�A2���ٹ�A2��ֱ��A2B2��x�ᣬ��y2��ͼ���ڵ�B2�����ν�����ȥ������A1A2��B1B2��A2A3��B2B3�������ǡ�A2A1B1�����ΪS1����A2B1B2�����ΪS2����A3A2B2�����ΪS3����A3B2B3�����ΪS4������S2016=31511��$\sqrt{3}$-1����
��ͼ����y����һ��P��0��1����ƽ����x���ֱ��PB���ֱ���y1=x2��x��0����y2=$\frac{{x}^{2}}{3}$��x��0����ͼ����A1��B1���㣬����B1��y���ƽ���߽�y1��ͼ���ڵ�A2���ٹ�A2��ֱ��A2B2��x�ᣬ��y2��ͼ���ڵ�B2�����ν�����ȥ������A1A2��B1B2��A2A3��B2B3�������ǡ�A2A1B1�����ΪS1����A2B1B2�����ΪS2����A3A2B2�����ΪS3����A3B2B3�����ΪS4������S2016=31511��$\sqrt{3}$-1����
���� �ȸ��ݵ�P�������������A1��B1��A2��B2��A3��B3��A4��B4�����꣬�Ӷ����A1B1��A2B1��A2B2��A3B2��A3B3��A4B3�ij������������������ʽ���S1��S2��S3��S4��S5��ֵ������֪S3=3$\sqrt{3}$S1��S5=3$\sqrt{3}$S3�������ݴ˹��ɽ�ɣ�
��� �⣺��ͼ��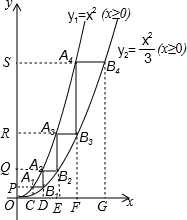
��y=1ʱ����x2=1 ��x��0�����ã�x=1������A1��1��1����
��$\frac{{x}^{2}}{3}$=1��x��0�����ã�x=$\sqrt{3}$����B1��$\sqrt{3}$��1����
��x=$\sqrt{3}$ʱ��y=x2=��$\sqrt{3}$��2=3����A2��$\sqrt{3}$��3����
��A1B1=$\sqrt{3}$-1��A2B1=2��
��y=3ʱ����$\frac{{x}^{2}}{3}$=3��x��0�����ã�x=3����B2��3��3����
��x=3ʱ��y=x2=32=9����A3��3��9����
��A2B2=3-$\sqrt{3}$��A3B2=6��
��y=9ʱ����$\frac{{x}^{2}}{3}$=9��x��0�����ã�x=3$\sqrt{3}$����B3��3$\sqrt{3}$��9����
��A3B3=3$\sqrt{3}$-3��
��x=3$\sqrt{3}$ʱ��y=x2=��3$\sqrt{3}$��2=27����A4��3$\sqrt{3}$��27����
��A4B3=18��
��y=27�ǣ���$\frac{{x}^{2}}{3}$=27��x��0�����ã�x=9����B4��9��27����
��A4B4=9-3$\sqrt{3}$��
��S1=$\frac{1}{2}$��2����$\sqrt{3}$-1��=$\sqrt{3}$-1��
S2=$\frac{1}{2}$��2����3-$\sqrt{3}$��=3-$\sqrt{3}$=$\sqrt{3}$��$\sqrt{3}$-1����
S3=$\frac{1}{2}$��6����3-$\sqrt{3}$��=3��3-$\sqrt{3}$��=3$\sqrt{3}$��$\sqrt{3}$-1����
S4=$\frac{1}{2}$��6����3$\sqrt{3}$-3��=9��$\sqrt{3}$-1����
S5=$\frac{1}{2}$��18����3$\sqrt{3}$-3��=27��3$\sqrt{3}$-3��=��3$\sqrt{3}$��2����$\sqrt{3}$-1����
��S2015=$��3\sqrt{3}��^{\frac{2015-1}{2}}$����$\sqrt{3}$-1��=��3$\sqrt{3}$��1007��$\sqrt{3}$-1����
S2016=$\sqrt{3}$•S2015=��3$\sqrt{3}$��1007��$\sqrt{3}$-1����$\sqrt{3}$=31511��$\sqrt{3}$-1����
�ʴ�Ϊ��31511��$\sqrt{3}$-1����
���� ������Ҫ������κ���ͼ���ϵ����������������ֵı仯���ɣ����������߽���ʽ��ø���������������ĸ������г��������ε�����������б仯�����ǽ���Ĺؼ���

| A�� | $\frac{60-4}{0.8x}$=$\frac{60}{x}$+1 | B�� | $\frac{60-4}{x}$=$\frac{60}{0.8x}$+1 | C�� | $\frac{60}{0.8x}$=$\frac{60-4}{x}$+1 | D�� | $\frac{60-4}{x}$=$\frac{60}{0.8x}$-1 |
 ��ͼ�����ɱ߳�Ϊ1��С��������ɵ������У���ABC������������ڸ���ϣ��밴Ҫ��������и��⣺
��ͼ�����ɱ߳�Ϊ1��С��������ɵ������У���ABC������������ڸ���ϣ��밴Ҫ��������и��⣺