题目内容
三个连续的正奇数,最大数与最小数的积比中间的一个数的6倍多3,求这三个数.
考点:一元二次方程的应用
专题:数字问题
分析:设出三个连续正奇数,利用等量关系:最大数与最小数的积比中间的一个数的6倍多3列出方程,即可解决问题.
解答:解:设中间的正奇数为x,
则另外两个正奇数为:x-2,x+2;
由题意得:(x-2)(x+2)=6x+3,
整理得:x2-6x-7=0,
解得:x1=7,x2=-1(不合题意,舍去),
所以此三个数为5,7,9.
则另外两个正奇数为:x-2,x+2;
由题意得:(x-2)(x+2)=6x+3,
整理得:x2-6x-7=0,
解得:x1=7,x2=-1(不合题意,舍去),
所以此三个数为5,7,9.
点评:考查了一元二次方程的应用问题;解题的关键是正确设出未知数,利用命题中给出的等量关系列出方程,然后求解.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
2015年南箐小学的营养餐费用大约用去1370000元,将1370000用科学记数法表示为( )
| A、137×104 |
| B、13.7×105 |
| C、1.37×106 |
| D、1.37×104 |
若关于x的函数y=kx2+2x-1与x轴只有一个交点,则实数k的值为( )
| A、-1 | B、-2 | C、1 | D、2 |
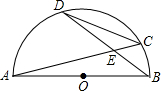 半圆O的直径AB=9,两弦AB、CD相交于点E,弦CD=
半圆O的直径AB=9,两弦AB、CD相交于点E,弦CD=| 27 |
| 5 |
| A、5 | ||||
| B、4 | ||||
C、3
| ||||
D、
|
 如图所示,AB为⊙O的直径,点C在⊙O上,若∠A=15°,则∠BOC的度数是( )
如图所示,AB为⊙O的直径,点C在⊙O上,若∠A=15°,则∠BOC的度数是( )| A、15° | B、30° |
| C、45° | D、75° |
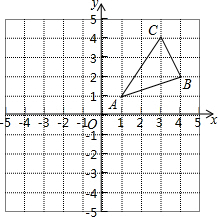 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4). 如图,已知,⊙O的半径为3cm,过直径BA延长线上一点P作直线分别交⊙O于点C,D,若C是PD的中点,且PC=2PA,求PA的长.
如图,已知,⊙O的半径为3cm,过直径BA延长线上一点P作直线分别交⊙O于点C,D,若C是PD的中点,且PC=2PA,求PA的长.