题目内容
 如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD上任意一点,将BM绕点B逆时针旋转60°得到BN,连接BN、AM、CM.
如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD上任意一点,将BM绕点B逆时针旋转60°得到BN,连接BN、AM、CM.(1)求证:△AMB≌△ENB;
(2)若正方形的边长为
| 2 |
考点:正方形的性质,全等三角形的判定与性质,旋转的性质
专题:
分析:(1)由题意得MB=NB,∠ABN=15°,所以∠EBN=45°,容易证出△AMB≌△ENB;
(2)顺时针旋转△BPC60度,可得△PBE为等边三角形,若PA+PB+PC=AP+PE+EF要使最小只要AP,PE,EF在一条直线上,求出AF的值即可
(2)顺时针旋转△BPC60度,可得△PBE为等边三角形,若PA+PB+PC=AP+PE+EF要使最小只要AP,PE,EF在一条直线上,求出AF的值即可
解答:
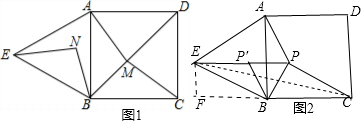 解:(1)如图1,∵四边形ABCD为正方形,△ABE为等边三角形,
解:(1)如图1,∵四边形ABCD为正方形,△ABE为等边三角形,
∴BE=BA,BA=BC,∠ABE=60°;
∵∠MBN=60°,
∴BE=BA,∠MBN=∠ABE,
∴∠MBA=∠NBE;
在△AMB与△ENB中,
,
 ∴△AMB≌△ENB(SAS),
∴△AMB≌△ENB(SAS),
(2)顺时针旋转△BPC60度,可得△PBE为等边三角形.
即得PA+PB+PC=AP+PE+EF要使最小只要AP,PE,EF在一条直线上,
即如下图:可得最小PA+PB+PC=AF.
BM=BF•cos30°=BC•cos30°=
,
则AM=
+
=
,
∵AB=BF,∠ABF=150°
∴∠BAF=15°
既得AF=
=
-1.
 解:(1)如图1,∵四边形ABCD为正方形,△ABE为等边三角形,
解:(1)如图1,∵四边形ABCD为正方形,△ABE为等边三角形,∴BE=BA,BA=BC,∠ABE=60°;
∵∠MBN=60°,
∴BE=BA,∠MBN=∠ABE,
∴∠MBA=∠NBE;
在△AMB与△ENB中,
|
 ∴△AMB≌△ENB(SAS),
∴△AMB≌△ENB(SAS),(2)顺时针旋转△BPC60度,可得△PBE为等边三角形.
即得PA+PB+PC=AP+PE+EF要使最小只要AP,PE,EF在一条直线上,
即如下图:可得最小PA+PB+PC=AF.
BM=BF•cos30°=BC•cos30°=
| ||
| 2 |
则AM=
| 2 |
| ||
| 2 |
2
| ||||
| 2 |
∵AB=BF,∠ABF=150°
∴∠BAF=15°
既得AF=
| AM |
| cos15° |
| 3 |
点评:本题主要考查轴对称-路线最短问题、正方形的性质及旋转的性质,解答本题的关键是熟练掌握旋转的知识,此题难度一般.

练习册系列答案
相关题目
若方程x2-(m2-4)x+m=0的两个实根互为相反数,则m的值是( )
| A、0 | B、2 | C、-2 | D、-2或2 |
下列各式中正确的是( )
| A、3a2-2a2=1 |
| B、5a+2b=7ab |
| C、-2(a-b)=-2a-b |
| D、3x+5x=8x |
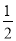 C.
C. D.
D.
 在正方形ABCD中,点P是对角线AC上一点,PE⊥AB,PF⊥BC,垂足分别是E、F.
在正方形ABCD中,点P是对角线AC上一点,PE⊥AB,PF⊥BC,垂足分别是E、F.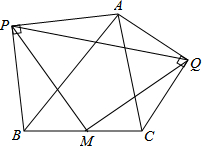 如图,在锐角△ABC的边上分别作等腰Rt△ABP和等腰Rt△AQC.其中∠APB、∠AQC都是直角,M是BC中点,连PM、QM、PQ.求证:△PMQ为等腰三角形.
如图,在锐角△ABC的边上分别作等腰Rt△ABP和等腰Rt△AQC.其中∠APB、∠AQC都是直角,M是BC中点,连PM、QM、PQ.求证:△PMQ为等腰三角形.