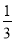题目内容
解方程:(1) 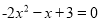 ; (2)
; (2)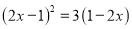 .
.
【答案】(1)x1 =1 ,x2= ; (2) x1 =-1,x2=
; (2) x1 =-1,x2=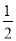 .
.
【解析】试题分析:
根据两方程的特点,使用“因式分解法”解两方程即可.
试题解析:
(1)原方程可化为: 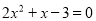 ,
,
方程左边分解因式得: 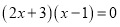 ,
,
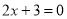 或
或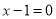 ,
,
解得: 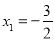 ,
, 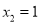 .
.
(2)原方程可化为: 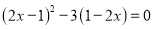 ,即
,即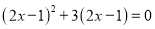 ,
,
∴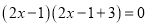 ,
,
∴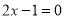 或
或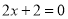 ,
,
解得: 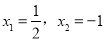 .
.
【题型】解答题
【结束】
20
已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
(1)m的值为6;(2)17. 【解析】试题分析: (1)由题意和根与系数的关系可得:x1+x2=2(m+1),x1x2=m2+5;由(x1-1)(x2-1)=28,可得:x1x2-(x1+x2)=27;从而得到:m2+5-2(m+1)=27,解方程求得m的值,再由“一元二次方程根的判别式”进行检验即可得到m的值; (2)①当7为腰长时,则方程的两根中有一根为7,代入方程可解得m...
练习册系列答案
相关题目


 +1)关于原点的对称点在第四象限,则a的取值范围在数轴上表示正确的是( )
+1)关于原点的对称点在第四象限,则a的取值范围在数轴上表示正确的是( ) B.
B. 
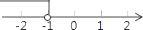 D.
D. 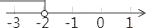
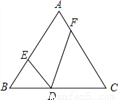
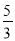
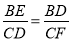 ,由已知易得:CD=BC-BD=5-1=4,由此可得:
,由已知易得:CD=BC-BD=5-1=4,由此可得: 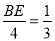 ,解得BE=
,解得BE=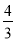 .
.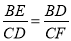 ,即
,即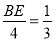 ,
,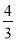 .
.
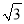 .
.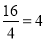 ,
,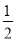 AD=2,
AD=2,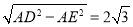 ,
, DE=
DE=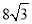 .
.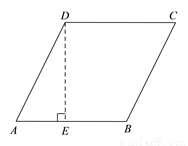
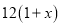 ,
,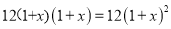 ,
,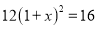 .
.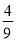 B.
B. 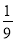 C.
C. 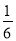 D.
D.