下列实数中是无理数的是( )A．tan30°B．$\root{3}{8}$C．$\frac{1}{3}$D．$\sqrt{49}$ 题目和参考答案——青夏教育精英家教网—

题目内容

1．下列实数中是无理数的是（　　）

A．

tan30°

B．

$\root{3}{8}$

C．

$\frac{1}{3}$

D．

$\sqrt{49}$

分析根据无理数的三种形式求解即可．

解答解：tan30°=$\frac{\sqrt{3}}{3}$，$\root{3}{8}$=2，$\sqrt{49}$=7，
无理数为：$\frac{\sqrt{3}}{3}$．
故选A．

点评本题考查了无理数的知识，解答本题的关键是掌握无理数的三种形式：①开方开不尽的数，②无限不循环小数，③含有π的数．

练习册系列答案

相关题目

11．连接四边形任意不相邻的两个顶点的线段叫做四边形的对角线，如图：

从四边形的一个顶点可以引出 1 条对角线，把四边形分成 2 个三角形；
从五边形的一个顶点可以引出 2 条对角线，把五边形分成 3 个三角形；
从六边形的一个顶点可以引出 3 条对角线，把六边形分成 4个三角形；
…
从n边形的一个顶点可以引出（n-3）条对角线，把n边形分成（n-2）个三角形；
已知任意三角形的内角和为180°，则：
四边形的内角和为：180°×2
五边形的内角和为：180°×3
六边形的内角和为：180°×4
…
n边形的内角和为：（n-2）×180°（用含n的代数式表示）
根据上面你所找到的规律尝试计算十二边形的内角和，你一定能行．

12．

小军利用一张圆心角为90°，半径为20cm的扇形皮纸制作了一顶圆锥形纸帽（如下面的示意图），按照1：5的比例尺画出纸帽的三视图并标注数据．

9．

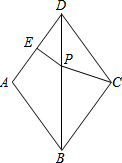如图，在菱形ABCD中，∠ADC=72°，AD的垂直平分线交对角线BD于点P，垂足为E，连接CP，则∠CPB的度数是（　　）

	A．	二元一次方程x+2y=2的解可以表示为$\left\{\begin{array}{l}{x=m}\\{y=1-\frac{m}{2}}\end{array}\right.$ （m是实数）
	B．	若$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}{3x+2y=m}\\{nx-y=1}\end{array}\right.$的解，则m+n的值为0
	C．	设一元二次方程x²+3x-4=0的两根分别为m、n，则m+n的值为-3
	D．	若-5x²y^m与xⁿy是同类项，则m+n的值为3

13．

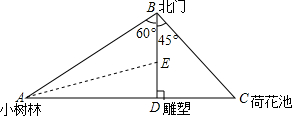某公园有一座雕塑D，在北门B的正南方向，BD为100米，小树林A在北门的南偏西60°方向，荷花池C在北门B的东南方向，已知A，D，C三点在同一条直线上且BD⊥AC：
（1）分别求线段AB、BC、AC的长（结果中保留根号，下同）；
（2）若有一颗银杏树E恰好位于∠BAD的平分线与BD的交点，求BE的距离．

10．已知方程组$\left\{\begin{array}{l}{{x}^{2}+2{y}^{2}=m}\\{3xy=n}\end{array}\right.$的一组解为$\left\{\begin{array}{l}{{x}_{1}=3}\\{{y}_{1}=-2}\end{array}\right.$，则这个方程组的其他解为$\left\{\begin{array}{l}{{x}_{1}=-3}\\{{y}_{1}=2}\end{array}\right.$，$\left\{\begin{array}{l}{{x}_{2}=2\sqrt{2}}\\{{y}_{2}=-\frac{3}{2}\sqrt{2}}\end{array}\right.$，$\left\{\begin{array}{l}{{x}_{3}=-2\sqrt{2}}\\{{y}_{3}=\frac{3}{2}\sqrt{2}}\end{array}\right.$．

11．下列语句中，正确的个数是（　　）
（1）等腰三角形的对称轴是底边的垂直平分线；（2）菱形的对角线相等且互相平分；（3）四个内角都相等的四边形是矩形；（4）顺次连接对角线相等的四边形各边中点所得的四边形是菱形；（5）对角线互相垂直且相等的四边形是正方形．

试题分类