Question

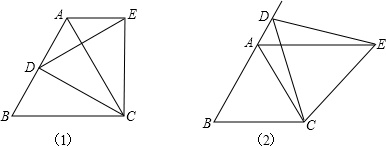
20．如图，在△ABC中，∠ABC，∠ACB的角平分线相交于点O，过点O作DE∥BC分别交AB、AC于D、E两点，AB=6，AC=8，则△ADE的周长是14．

Answer 1

分析 由BO平分∠ABC，CO平分∠ACB，过点O作DE∥BC，易得△BOD与△COE是等腰三角形，即可得△ADE的周长等于AB+AC，又由AB=6，AC=8，即可求得答案．

解答 解：∵BO平分∠ABC，CO平分∠ACB，
∴∠ABO=∠OBC，∠ACO=∠OCB，
∵DE∥BC，
∴∠BOD=∠OBC，∠COE=∠OCB，
∴∠ABO=∠BOD，∠ACO=∠COE，
∴BD=OD，CE=OE，
∵AB=6，AC=8，
∴△ADE的周长为：AD+DE+AE=AD+OD+OE+AE=AD+BD+CE+AE=AB+AC=6+8=14．
故答案为：14．

点评 本题考查三角形的内角和定理，等腰三角形的性质，平行线的性质及角平分线的性质，整体思想的利用和有效的进行线段的等量代换是正确解答本题的关键．