题目内容
 24、(1)如图,以△ABC三边向外分别作等边△ACD、△ABE、△BCF,判断四边形ADFE的形状;
24、(1)如图,以△ABC三边向外分别作等边△ACD、△ABE、△BCF,判断四边形ADFE的形状;(2)在(1)中,是否存在平行四边形ADFE?若存在,写出△ABC应满足的条件;若不存在,请说明理由;
(3)△ABC满足什么条件时,四边形ADFE是矩形?
(4)△ABC满足什么条件时,四边形ADFE是菱形?
(5)△ABC满足什么条件时,四边形ADFE是正方形?
分析:(1)可通过证△EFB≌△ACB,得EF=AC=AD;然后证△CDF≌△CAB,得DF=AB=AE;从而证得四边形ADFE的两组对边分别相等,即可得出ADFE是平行四边形;
(2)由(1)知四边形ADEF是平行四边形,那么只需AEFD能构成四边形即可,所以E、A、D不能共线,即∠BAC≠60°;
(3)当ADFE是矩形时,∠EAD=90°,由此可求得∠BAC的度数;
(4)当ADFE是菱形时,AE=AD,此时AB=AC;
(5)当ADFE是正方形时,∠EAD=90°,且AE=AD,联立(3)(4)的结论即可.
(2)由(1)知四边形ADEF是平行四边形,那么只需AEFD能构成四边形即可,所以E、A、D不能共线,即∠BAC≠60°;
(3)当ADFE是矩形时,∠EAD=90°,由此可求得∠BAC的度数;
(4)当ADFE是菱形时,AE=AD,此时AB=AC;
(5)当ADFE是正方形时,∠EAD=90°,且AE=AD,联立(3)(4)的结论即可.
解答:解:(1)∵△ABE、△CBF是等边三角形,
∴BE=AB,BF=CB,∠EBA=∠FBC=60°;
∴∠EBF=∠ABC=60°-∠EBA;
∴△EFB≌△ACB;
∴EF=AC=AD;
同理由△CDF≌△CAB,得DF=AB=AE;
由AE=DF,AD=EF即可得出四边形AEFD是平行四边形;
(2)存在,且△ABC需满足的条件是∠BAC≠60°;
证明:当∠BAC=60°时,
∵△ABE、△ACD是等边三角形,
∴∠BAE=∠CAD=60°;
若∠BAC=60°,
则E、A、D三点共线,A、E、F、D够不成四边形;
当∠BAC≠60°时,由(1)知四边形AEFD是平行四边形;
故存在平行四边形AEFD,且△ABC需满足的条件是∠BAC≠60°;
(3)若平行四边形AEFD是矩形,则∠EAD=90°;
∴∠BAC=360°-90°-60°-60°=150°;
即△ABC满足∠BAC=150°时,四边形AEFD是矩形;
(4)若平行四边形AEFD是菱形,则AE=AD;
此时AE=AB=AC=AD,即△ABC是等腰三角形;
故△ABC满足AB=AC时,四边形AEFD是菱形;
(5)综合(3)(4)的结论知:当△ABC是顶角∠BAC是150°的等腰三角形时,四边形AEFD是正方形.
∴BE=AB,BF=CB,∠EBA=∠FBC=60°;
∴∠EBF=∠ABC=60°-∠EBA;
∴△EFB≌△ACB;
∴EF=AC=AD;
同理由△CDF≌△CAB,得DF=AB=AE;
由AE=DF,AD=EF即可得出四边形AEFD是平行四边形;
(2)存在,且△ABC需满足的条件是∠BAC≠60°;
证明:当∠BAC=60°时,
∵△ABE、△ACD是等边三角形,
∴∠BAE=∠CAD=60°;
若∠BAC=60°,
则E、A、D三点共线,A、E、F、D够不成四边形;
当∠BAC≠60°时,由(1)知四边形AEFD是平行四边形;
故存在平行四边形AEFD,且△ABC需满足的条件是∠BAC≠60°;
(3)若平行四边形AEFD是矩形,则∠EAD=90°;
∴∠BAC=360°-90°-60°-60°=150°;
即△ABC满足∠BAC=150°时,四边形AEFD是矩形;
(4)若平行四边形AEFD是菱形,则AE=AD;
此时AE=AB=AC=AD,即△ABC是等腰三角形;
故△ABC满足AB=AC时,四边形AEFD是菱形;
(5)综合(3)(4)的结论知:当△ABC是顶角∠BAC是150°的等腰三角形时,四边形AEFD是正方形.
点评:熟练掌握个特殊四边形的判定方法和性质是解答此题的关键.

练习册系列答案
相关题目
 如图是以AB为直径的半圆弧ADB和圆心角为45°的扇形ABC,则图中Ⅰ的面积和Ⅱ的面积的比值是( )
如图是以AB为直径的半圆弧ADB和圆心角为45°的扇形ABC,则图中Ⅰ的面积和Ⅱ的面积的比值是( )| A、1.6 | B、1.4 | C、1.2 | D、1 |
 请说明理由.
请说明理由.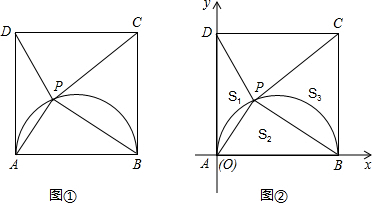
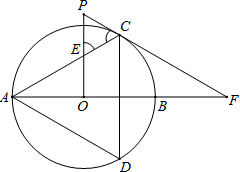 (2012•茂名)如图,以AB为直径的⊙O是△ADC的外接圆,过点O作PO⊥AB,交AC于点E,PC的延长线交AB的延长线于点F,∠PEC=∠PCE.
(2012•茂名)如图,以AB为直径的⊙O是△ADC的外接圆,过点O作PO⊥AB,交AC于点E,PC的延长线交AB的延长线于点F,∠PEC=∠PCE. 如图,以AB为直径的⊙O经过点P,C是⊙O上一点,连接PC交AB于点E,且∠ACP=60°,PA=PD.
如图,以AB为直径的⊙O经过点P,C是⊙O上一点,连接PC交AB于点E,且∠ACP=60°,PA=PD.