题目内容
13.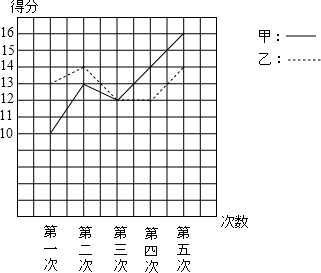 甲、乙两人参加某体育项目训练,近期的五次测试成绩得分情况如图.
甲、乙两人参加某体育项目训练,近期的五次测试成绩得分情况如图.(1)分别求出两人得分的平均数、中位数与方差;
(2)根据上面写出的结果,对两人的训练成绩从不同方面分别作出评价.
(3)现要从甲、乙两人中挑选一人参加比赛,如果仅从得分成绩的图象趋势考虑,你认为选择谁参加比较为合适?请说明理由.
分析 (1)根据平均数、方差、中位数的定义进行计算即可;
(2)根据计算的平均数、中位数以及方差来评价即可;
(3)从折线图上明显可以看出甲的成绩上升较快,乙得比较迟缓,故选甲.
解答 解:(1)甲五次测试成绩是10,13,12,14,16,
乙五次测试成绩是13,14,12,12,14.
甲平均数13,甲中位数13,甲方差4;
乙平均数13,乙中位数13,乙方差0.8.
(2)∵甲平均数=乙平均数,∴从平均数看,甲、乙成绩一样;
∵甲中位数=乙中位数,∴从中位数看,甲、乙成绩一样;
∵甲方差>乙方差,∴从稳定性看,乙成绩更稳定.
(3)甲成绩呈现一种上升状态,不断提高,乙成绩上下波动,无明显提高,
∴从成绩图象的趋势看,应选甲参加合适.
点评 本题考查了方差、平均数以及中位数,掌握方差、平均数以及中位数的计算方法,以及它们的特征是解题的关键.

练习册系列答案
相关题目
3.若二次三项式x2+bx+c是一个完全平方式,则数b、c满足的关系是( )
| A. | b=2,c=1 | B. | b=4c | C. | b2=4c | D. | c2=4b |
4.期中考试后,班里有两位同学议论他们所在小组同学的数学成绩,甲说:“我们组成绩是88分的同学最多”,乙说:“我们组的11位同学成绩排在最中间的恰好也是88分”,上面两位同学的话能反映出的统计量分别是( )
| A. | 众数和平均数 | B. | 平均数和中位数 | C. | 众数和方差 | D. | 众数和中位数 |
1.下列说法不正确的是( )
| A. | 对角线互相垂直的矩形一定是正方形 | |
| B. | 对角线相等的菱形一定是正方形 | |
| C. | 对角线互相垂直且相等的平行四边形一定是正方形 | |
| D. | 顺次连接任意对角线相等的四边形的各边中点所得的四边形一定是正方形 |
5. 如图,在平面直角坐标系xOy中,点P(-3,5)关于x轴的对称点坐标为( )
如图,在平面直角坐标系xOy中,点P(-3,5)关于x轴的对称点坐标为( )
 如图,在平面直角坐标系xOy中,点P(-3,5)关于x轴的对称点坐标为( )
如图,在平面直角坐标系xOy中,点P(-3,5)关于x轴的对称点坐标为( )| A. | (-3,-5) | B. | (3,5) | C. | (3,-5) | D. | (5,-3) |
2.下列运算正确的是( )
| A. | x2+x2=2x4 | B. | (3y)2=6y2 | C. | (x2)3=x6 | D. | (x+y)2=x2+y2 |
3.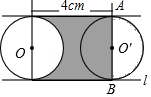 如图,经直径为3cm的⊙O沿直线l平移4cm到⊙O′,AB为⊙O′的直径,则图中阴影部分面积为( )
如图,经直径为3cm的⊙O沿直线l平移4cm到⊙O′,AB为⊙O′的直径,则图中阴影部分面积为( )
 如图,经直径为3cm的⊙O沿直线l平移4cm到⊙O′,AB为⊙O′的直径,则图中阴影部分面积为( )
如图,经直径为3cm的⊙O沿直线l平移4cm到⊙O′,AB为⊙O′的直径,则图中阴影部分面积为( )| A. | 6cm2 | B. | (12-$\frac{9}{8}$π)cm2 | C. | 18cm2 | D. | ($\frac{9}{8}$π+6)cm2 |
 如图,E、F分别为?ABCD的边BC、AD上的点,且∠1=∠2.求证:四边形AECF是平行四边形.
如图,E、F分别为?ABCD的边BC、AD上的点,且∠1=∠2.求证:四边形AECF是平行四边形.