题目内容
1．下列说法不正确的是（ ）| A． | 对角线互相垂直的矩形一定是正方形 | |
| B． | 对角线相等的菱形一定是正方形 | |
| C． | 对角线互相垂直且相等的平行四边形一定是正方形 | |
| D． | 顺次连接任意对角线相等的四边形的各边中点所得的四边形一定是正方形 |
分析 直接利用中点四边形的判定方法以及结合正方形的判定方法、矩形、菱形、平行四边形的性质分别分析得出答案．
解答 解：A、对角线互相垂直的矩形一定是正方形，正确，不合题意；
B、对角线相等的菱形一定是正方形，正确，不合题意；
C、对角线互相垂直且相等的平行四边形一定是正方形，正确，不合题意；
D、顺次连接任意对角线相等的四边形的各边中点所得的四边形一定是菱形，故此选项错误，符合题意．
故选：D．
点评 此题主要考查了中点四边形的判定方法以及正方形的判定方法、矩形、菱形、平行四边形的性质，正确把握相关正方形的判定方法是解题关键．
练习册系列答案
相关题目
11．下列事件属于确定事件的是（ ）
| A． | 掷一枚质地均匀的骰子，掷出的点数是奇数 | |
| B． | 车辆随机经过一个路口，遇到红灯 | |
| C． | 若两数之和是负数，则其中至少有一个加数是负数 | |
| D． | 有三条线段，将这三条线段首尾顺次相接可以组成一个三角形 |
（1）如图，在?ABCD中，点E，F分别在AB，CD上，AE=CF．求证：DE=BF．
9．某篮球队对运动员进行3分球投篮成绩测试，每人每天投3分球10次，对甲，乙两名队员在五天中进球的个数统计结果如下：
经过计算，甲进球的平均数为${\overline{x}}_{甲}$=8，方差为S甲2=3.2．
（1）求乙进球的平均数${\overline{x}}_{乙}$和方差S乙2；
（2）现在需要根据以上结果，从甲，乙两名队员中选出一人去参加3分球投篮大赛，你认为应该选哪名队员去？为什么？
| 队员 | 每人每天进球数 | ||||
| 甲 | 10 | 6 | 10 | 6 | 8 |
| 乙 | 7 | 9 | 7 | 8 | 9 |
（1）求乙进球的平均数${\overline{x}}_{乙}$和方差S乙2；
（2）现在需要根据以上结果，从甲，乙两名队员中选出一人去参加3分球投篮大赛，你认为应该选哪名队员去？为什么？
16．点A（-3，-6）向上平移3个单位，再向左平移2个单位到点B，则点B的坐标为（ ）
| A． | （0，-2） | B． | （-5，-8） | C． | （-5，-3） | D． | （0，-3） |
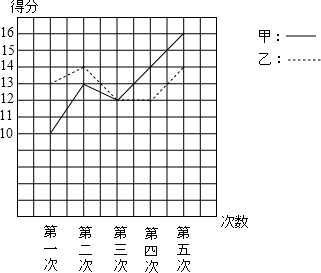甲、乙两人参加某体育项目训练，近期的五次测试成绩得分情况如图．
如图，E，F为平行四边形ABCD的对角线BD上的两点，AE⊥BD于点E，CF⊥BD于点F．