题目内容
15.已知关于x的方程(k+1)x2+(3k-1)x+2k-2=0(1)求证:无论k取何值,此方程总有实数根;
(2)若抛物线y=(k+1)x2+(3k-1)x+2k-2必通过两个定点,求这两个定点坐标;
(3)若此方程有两个整数根,求正整数k的值;
(4)若抛物线y=(k+1)x2+(3k-1)x+2k-2与x轴的两个交点之间的距离为3,求k的值.
分析 (1)分k=-1和k≠-1两种情况讨论方程根的情况即可;
(2)把线y=(k+1)x2+(3k-1)x+2k-2转化为y=k(x+1)(x+2)+x2-x-2,进而求出两个定点;
(3)求出方程两根,一根为-1,另一根为2-$\frac{4k}{k+1}$,根据方程两根均为整数,即可求出k的值;
(4)根据抛物线与x轴的两个交点之间的距离为3,即两根之差的绝对值为3,据此求出k的值.
解答 解:(1)当k=-1时,方程为-4x-4=0是一元一次方程,有一个实数根;
当k≠-1时,△=(3k-1)2-4(k+1)(2k-2)=(k-3)2≥0,此时方程有两个实数根.
综上所述,无论k取何值,此方程总有实数根.
(2)∵y=(k+1)x2+(3k-1)x+2k-2,
∴y=k(x+1)(x+2)+x2-x-2,
∴当x=-1时,y=0,当x=-2时,y=4,
∴这两个定点坐标(-1,0)、(-2,4);
(3)∵方程有一根为x=-1,
则另一根为x=$\frac{2-k}{k+1}$=2-$\frac{4k}{k+1}$,
∵方程的两个根是整数,k为正整数,
∴k=1或3;
(4)依题意得x1-x2=3或x2-x1=3,
当-1-(2-$\frac{4k}{k+1}$)=3时,
解得k=-3;
当(2-$\frac{4k}{k+1}$)-(-1)=3时,
解得k=0,
综上k=-3或0.
点评 本题主要考查了抛物线与x轴交点、二次函数图象上点的坐标特征以及根的判别式的知识,解答本题的关键是抛物线与坐标交点和根的判别式的关系,此题难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.对于分式$\frac{{x}^{2}+1}{{x}^{2}+2x+2}$,下列说法错误的是( )
| A. | 不论x取何值,分式都有意义 | B. | 分式的值可以等于1 | ||
| C. | 不论x取何值,分式值都不为0 | D. | 当x=0或-1时,分式无意义 |
20.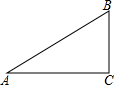 如图在Rt△ABC中,∠C=90°,AB=15,sinA=$\frac{1}{3}$,则BC等于( )
如图在Rt△ABC中,∠C=90°,AB=15,sinA=$\frac{1}{3}$,则BC等于( )
 如图在Rt△ABC中,∠C=90°,AB=15,sinA=$\frac{1}{3}$,则BC等于( )
如图在Rt△ABC中,∠C=90°,AB=15,sinA=$\frac{1}{3}$,则BC等于( )| A. | 45 | B. | 5 | C. | $\frac{1}{5}$ | D. | $\frac{1}{45}$ |
14.已知:AB⊥CD,垂足为O,EF经过点O,∠AOE=35°,则∠DOF等于( )
| A. | 65° | B. | 55°或125° | C. | 35° | D. | 65°或155° |
 如图,正方形ABCD中,点O是对角线AC的中点,点P是线段AO上的动点(不与点A、O重合),连结PB,作PE⊥PB交CD于点E.以下结论:①△PBC≌△PDC;②∠PDE=∠PED;③PC-PA=$\sqrt{2}$CE.其中正确的有( )个.
如图,正方形ABCD中,点O是对角线AC的中点,点P是线段AO上的动点(不与点A、O重合),连结PB,作PE⊥PB交CD于点E.以下结论:①△PBC≌△PDC;②∠PDE=∠PED;③PC-PA=$\sqrt{2}$CE.其中正确的有( )个.