题目内容
6.已知关于x的一元二次方程(x-k)2-2x+2k=0有两个实数根x1、x2.(1)求实数k的取值范围;
(2)当实数k为何值时,代数式x12+x22-x1•x2+1取得最小值,并求出该最小值.
分析 (1)先把方程整理为一般式,然后计算判别式的值得到△=4>0,于是根据判别式的意义可得k为任意实数;
(2)根据根与系数的关系得到x1+x2=2(k+1),x1x2=k2+2k,则x12+x22-x1•x2+1=(x1+x2)2-3x1x2+1=4(k+1)2-3(k2+2k)+1,然后整理后配方得到(k+1)2+4,再利用非负数的性质确定最小值.
解答 解:(1)方程整理得x2-2(k+1)+k2+2k=0,
∵△=4(k+1)2-4(k2+2k)=4>0,
∴实数k的取值范围是任意实数;
(2)根据题意得x1+x2=2(k+1),x1x2=k2+2k,
x12+x22-x1•x2+1=(x1+x2)2-3x1x2+1=4(k+1)2-3(k2+2k)+1=k2+2k+5=(k+1)2+4,
当k=-1时,代数式x12+x22-x1•x2+1取得最小值,该最小值为4.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了判别式的意义.

练习册系列答案
相关题目
16.据悉,2015年我国将发展固定宽带接入新用户28 000 000户,28 000 000用科学记数法表示为( )
| A. | 28×106 | B. | 2.8×l06 | C. | 2.8×107 | D. | 0.28×l08 |
17.下列各数中,最小的数是( )
| A. | 0 | B. | 1 | C. | -$\sqrt{2}$ | D. | -1 |
1. 如图,点D为AC上一点,点O为边AB上一点,AD=DO.以O为圆心,OD长为半径作圆,交AC于另一点E,交AB于点F,G,连接EF.若∠BAC=22°,则∠EFG=( )
如图,点D为AC上一点,点O为边AB上一点,AD=DO.以O为圆心,OD长为半径作圆,交AC于另一点E,交AB于点F,G,连接EF.若∠BAC=22°,则∠EFG=( )
 如图,点D为AC上一点,点O为边AB上一点,AD=DO.以O为圆心,OD长为半径作圆,交AC于另一点E,交AB于点F,G,连接EF.若∠BAC=22°,则∠EFG=( )
如图,点D为AC上一点,点O为边AB上一点,AD=DO.以O为圆心,OD长为半径作圆,交AC于另一点E,交AB于点F,G,连接EF.若∠BAC=22°,则∠EFG=( )| A. | 55° | B. | 44° | C. | 38° | D. | 33° |
18.在下列算式中,运算结果正确的是( )
| A. | a2•a3=a6 | B. | a8÷a4=a4 | C. | 3a+$\sqrt{2}$a=3$\sqrt{2}$a | D. | (a-b)2=a2-b2 |
 如图,我市某中学在创建“特色校园”的活动中,将奉校的办学理念做成宣传牌(CD),放置在教学楼的顶部(如图所示)该中学数学活动小组在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿坡面AB向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度为i=1:$\sqrt{3}$,AB=10米,AE=15米.(i=1:$\sqrt{3}$是指坡面的铅直高度BH与水平宽度AH的比)
如图,我市某中学在创建“特色校园”的活动中,将奉校的办学理念做成宣传牌(CD),放置在教学楼的顶部(如图所示)该中学数学活动小组在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿坡面AB向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度为i=1:$\sqrt{3}$,AB=10米,AE=15米.(i=1:$\sqrt{3}$是指坡面的铅直高度BH与水平宽度AH的比)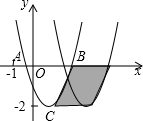 如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是③④.(写出所有正确结论的序号)
如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是③④.(写出所有正确结论的序号)