题目内容
7. 如图,正方形ABCD中,点O是对角线AC的中点,点P是线段AO上的动点(不与点A、O重合),连结PB,作PE⊥PB交CD于点E.以下结论:①△PBC≌△PDC;②∠PDE=∠PED;③PC-PA=$\sqrt{2}$CE.其中正确的有( )个.
如图,正方形ABCD中,点O是对角线AC的中点,点P是线段AO上的动点(不与点A、O重合),连结PB,作PE⊥PB交CD于点E.以下结论:①△PBC≌△PDC;②∠PDE=∠PED;③PC-PA=$\sqrt{2}$CE.其中正确的有( )个.| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 由正方形的性质得出BC=DC,∠BCP=∠DCP,由SAS即可证明△PBC≌△PDC,得出①正确;
由三角形全等得出∠PBC=∠PDE,PB=PD,再证出∠PBC=∠PED,得出∠PDE=∠PED,②正确;
证出PD=PE,得出DF=EF,作PH⊥AD于H,PF⊥CD于F,由等腰直角三角形得出PA=$\sqrt{2}$EF,PC=$\sqrt{2}$CF,即可得出③正确.
解答 解:∵四边形ABCD是正方形,
∴BC=DC,∠BCP=∠DCP,
在△PBC和△PDC中,
$\left\{\begin{array}{l}{BC=DC}&{\;}\\{∠BCP=∠DCP}&{\;}\\{PC=PC}&{\;}\end{array}\right.$,
∴△PBC≌△PDC(SAS)
∴①正确;
∴∠PBC=∠PDE,PB=PD,
∵PB⊥PE,∠BCD=90°,
∴∠PBC+∠PEC=360°-∠BPE-∠BCE=180°
∵∠PEC+∠PED=180°,
∴∠PBC=∠PED,
∴∠PDE=∠PED,
∴②正确;
∴PD=PE,
∵PF⊥CD,
∴DF=EF;
作PH⊥AD于点H,PF⊥CD于F,如图所示: 则PA=$\sqrt{2}$PH=$\sqrt{2}$DF=$\sqrt{2}$EF,PC=$\sqrt{2}$CF,
则PA=$\sqrt{2}$PH=$\sqrt{2}$DF=$\sqrt{2}$EF,PC=$\sqrt{2}$CF,
∴PC-PA=$\sqrt{2}$(CF-EF),
即PC-PA=$\sqrt{2}$CE,
∴③正确;
正确的个数有3个;
故选:D.
点评 本题考查了正方形的性质、全等三角形的判定与性质、等腰三角形的判定与性质、三角函数;本题有一定难度,特别是③中,需要作辅助线运用三角函数才能得出结果.

练习册系列答案
相关题目
17.下列各数中,最小的数是( )
| A. | 0 | B. | 1 | C. | -$\sqrt{2}$ | D. | -1 |
18.在下列算式中,运算结果正确的是( )
| A. | a2•a3=a6 | B. | a8÷a4=a4 | C. | 3a+$\sqrt{2}$a=3$\sqrt{2}$a | D. | (a-b)2=a2-b2 |
2. 某数学兴趣小组根据温州气象部门发布的有关数据,制作了PM2.5来源统计图,根据该统计图,下列判断正确的是( )
某数学兴趣小组根据温州气象部门发布的有关数据,制作了PM2.5来源统计图,根据该统计图,下列判断正确的是( )
 某数学兴趣小组根据温州气象部门发布的有关数据,制作了PM2.5来源统计图,根据该统计图,下列判断正确的是( )
某数学兴趣小组根据温州气象部门发布的有关数据,制作了PM2.5来源统计图,根据该统计图,下列判断正确的是( )| A. | 表示汽车尾气污染的圆心角约为72° | |
| B. | 表示建筑扬尘的约占6% | |
| C. | 汽车尾气污染约为建筑扬尘的5倍 | |
| D. | 煤炭以及其他燃料排放占所有PM2.5污染源的$\frac{1}{2}$ |
12.下列图形中,随机抽取一张是轴对称图形的概率是( )


| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
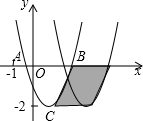 如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是③④.(写出所有正确结论的序号)
如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是③④.(写出所有正确结论的序号)