题目内容
 如图,⊙O半径是2
如图,⊙O半径是2| 3 |
| 6 |
分析:当PA⊥OA时,PA取最小值,∠OPA取得最大值,然后在直角三角形OPA中利用勾股定理求PA的值即可.
解答:解:在△OPA中,当∠OPA取最大值时,OA取最大值,
∴PA取最小值,
又∵OA、OP是定值,
∴PA⊥OA时,PA取最小值;
在直角三角形OPA中,OA=
,OP=2
,
∴PA=
=3
.
故选D.
∴PA取最小值,
又∵OA、OP是定值,
∴PA⊥OA时,PA取最小值;
在直角三角形OPA中,OA=
| 6 |
| 3 |
∴PA=
| 6+12 |
| 2 |
故选D.
点评:本题考查了解直角三角形.解答此题的关键是找出“当PA⊥OA时,PA取最小值”即“PA⊥OA时,∠OPA取最大值”这一隐含条件.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
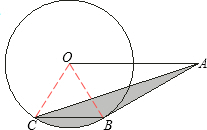 如图,A是半径为2的⊙O外的一点,OA=4,AB切⊙O于点B,弦BC∥OA,连接AC,则图中阴影部分的面积等于( )
如图,A是半径为2的⊙O外的一点,OA=4,AB切⊙O于点B,弦BC∥OA,连接AC,则图中阴影部分的面积等于( )A、
| ||||
B、
| ||||
| C、π | ||||
D、
|
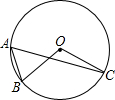 如图,⊙O是△ABC的外接圆,∠BAC=60°,若⊙O的半径0C为2,则弦BC的长为( )
如图,⊙O是△ABC的外接圆,∠BAC=60°,若⊙O的半径0C为2,则弦BC的长为( )| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
 如图,PA是⊙O的切线,PA=2
如图,PA是⊙O的切线,PA=2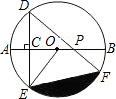 如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EF、EO,若DE=2
如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EF、EO,若DE=2