题目内容
若2xn+4y3与-3x2my2n+7的和仍是一个单项式,则(m+n)100= .
考点:合并同类项
专题:
分析:根据两者的和仍是一个单项式说明两式为同类项,根据同类项的字母相同及相同字母的指数相同可得出m和n的值,再代入计算即可.
解答:解:∵2xn+4y3与-3x2my2n+7的和仍是一个单项式,
∴n+4=2m,2n+7=3,
∴n=-2,m=1,
∴(m+n)100=(1-2)100=1;
故答案为:1.
∴n+4=2m,2n+7=3,
∴n=-2,m=1,
∴(m+n)100=(1-2)100=1;
故答案为:1.
点评:本题考查了合并同类项,难度不大,掌握同类项的字母相同及相同字母的指数相同是关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
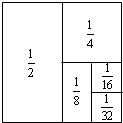 如图所示,将面积为1的长方形等分成两个面积为
如图所示,将面积为1的长方形等分成两个面积为
 如图,△ABC以点A为旋转中心,按逆时针方向旋转50°,得△AB′C′,则∠ABB′=
如图,△ABC以点A为旋转中心,按逆时针方向旋转50°,得△AB′C′,则∠ABB′= 电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体,若舞台AB长为20m,试计算主持人应走到离A点
电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体,若舞台AB长为20m,试计算主持人应走到离A点