题目内容
 二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是直线x=-1,则下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是直线x=-1,则下列四个结论:①b>0;②2a-b=0;③b2-4ac>0;④a+b+c>0中,
错误的有( )个.
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:二次函数图象与系数的关系
专题:数形结合
分析:由抛物线开口方向得到a<0,再根据抛物线的对称轴为直线x=-
=-1,得到b=2a,所以b<0,2a-b=0;根据抛物线与x轴的交点个数得到b2-4ac>0;
根据自变量为1时,对应的函数值小于0得到a+b+c<0.
| b |
| 2a |
根据自变量为1时,对应的函数值小于0得到a+b+c<0.
解答:解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=-
=-1,
∴b=2a,
∴b<0,所以①错误;
∴2a-b=0,所以②正确;
∵抛物线与x轴有两个交点,
∴b2-4ac>0,所以③正确;
∵当x=1时,y<0,
∴a+b+c<0,所以④错误.
故选B.
∴a<0,
∵抛物线的对称轴为直线x=-
| b |
| 2a |
∴b=2a,
∴b<0,所以①错误;
∴2a-b=0,所以②正确;
∵抛物线与x轴有两个交点,
∴b2-4ac>0,所以③正确;
∵当x=1时,y<0,
∴a+b+c<0,所以④错误.
故选B.
点评:本题考查了二次函数的图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=-
;抛物线与y轴的交点坐标为(0,c);当b2-4ac>0,抛物线与x轴有两个交点;当b2-4ac=0,抛物线与x轴有一个交点;当b2-4ac<0,抛物线与x轴没有交点.
| b |
| 2a |

练习册系列答案
相关题目
已知实数a,b,若a>b.则正确的是( )
| A、a-5<b-5 | ||||
| B、2+a<2+b | ||||
C、
| ||||
| D、-2a<-2b |
 如图是某几何体的三视图,其侧面积为( )
如图是某几何体的三视图,其侧面积为( )| A、4π | B、12π |
| C、16π | D、28π |
已知半径为5的⊙O中,弦AB=5,C是圆弧AB上的任意一点,则∠ACB等于( )
| A、30° |
| B、150° |
| C、30°或150° |
| D、30°或120° |
 有一三角形纸片ABC,∠A=80°,点D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得两纸片均为等腰三角形,则∠C的度数可以是
有一三角形纸片ABC,∠A=80°,点D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得两纸片均为等腰三角形,则∠C的度数可以是 如图,AB是⊙O的直径.弦CD⊥AB,交AB于点E,∠CDB=30°,⊙O的半径为2cm,求弦CD的长.
如图,AB是⊙O的直径.弦CD⊥AB,交AB于点E,∠CDB=30°,⊙O的半径为2cm,求弦CD的长. 如图,某中学教学楼BM上有一宣传牌AB,为了测量AB的高度,先在地面上用测角仪自C处测得宣传牌底部B的仰角是37°,然后将测角仪向教学楼方向移动了4m到达点F处,此时自E处测得宣传牌的顶部A的仰角为45°.已知测角仪的高度是1m,教学楼高17米,且点D,F、M在同一直线上,求宣传牌AB的高度(结果精确到0.1m,参考数据:sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).
如图,某中学教学楼BM上有一宣传牌AB,为了测量AB的高度,先在地面上用测角仪自C处测得宣传牌底部B的仰角是37°,然后将测角仪向教学楼方向移动了4m到达点F处,此时自E处测得宣传牌的顶部A的仰角为45°.已知测角仪的高度是1m,教学楼高17米,且点D,F、M在同一直线上,求宣传牌AB的高度(结果精确到0.1m,参考数据:sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).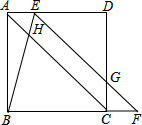 如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H,AE=CF,BE=EG.
如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H,AE=CF,BE=EG. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).