题目内容
 如图,某中学教学楼BM上有一宣传牌AB,为了测量AB的高度,先在地面上用测角仪自C处测得宣传牌底部B的仰角是37°,然后将测角仪向教学楼方向移动了4m到达点F处,此时自E处测得宣传牌的顶部A的仰角为45°.已知测角仪的高度是1m,教学楼高17米,且点D,F、M在同一直线上,求宣传牌AB的高度(结果精确到0.1m,参考数据:sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).
如图,某中学教学楼BM上有一宣传牌AB,为了测量AB的高度,先在地面上用测角仪自C处测得宣传牌底部B的仰角是37°,然后将测角仪向教学楼方向移动了4m到达点F处,此时自E处测得宣传牌的顶部A的仰角为45°.已知测角仪的高度是1m,教学楼高17米,且点D,F、M在同一直线上,求宣传牌AB的高度(结果精确到0.1m,参考数据:sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).考点:解直角三角形的应用-仰角俯角问题
专题:
分析:首先过点C作CN⊥AM于点N,则点C,E,N在同一直线上,设AB=x米,则AN=x+(17-1)=x+16(米),则在Rt△AEN中,∠AEN=45°,可得EN=AN=x+16,在Rt△BCN中,∠BCN=37°,BM=17,可得tan∠BCN=0.75,则可得方程,解此方程即可求得答案.
解答:解:过点C作CN⊥AM于点N,则点C,E,N在同一直线上,
设AB=x米,则AN=x+(17-1)=x+16(米),
在Rt△AEN中,∠AEN=45°,
∴EN=AN=x+16,
在Rt△BCN中,∠BCN=37°,BM=17,
∴tan∠BCN=
=0.75,
∴
=
,
解得:x=1
≈1.3.
经检验:x=1
是原分式方程的解.
答:宣传牌AB的高度约为1.3m.

设AB=x米,则AN=x+(17-1)=x+16(米),
在Rt△AEN中,∠AEN=45°,
∴EN=AN=x+16,
在Rt△BCN中,∠BCN=37°,BM=17,
∴tan∠BCN=
| BN |
| CN |
∴
| 17-1 |
| x+16+4 |
| 3 |
| 4 |
解得:x=1
| 1 |
| 3 |
经检验:x=1
| 1 |
| 3 |
答:宣传牌AB的高度约为1.3m.
点评:此题考查了仰角的定义.注意能借助仰角构造直角三角形并解直角三角形是解此题的关键.

练习册系列答案
相关题目
 如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第30秒时点E在量角器上对应的度数是( )
如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第30秒时点E在量角器上对应的度数是( )| A、60° | B、120° |
| C、90° | D、80° |
 二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是直线x=-1,则下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是直线x=-1,则下列四个结论:①b>0;②2a-b=0;③b2-4ac>0;④a+b+c>0中,
错误的有( )个.
| A、1个 | B、2个 | C、3个 | D、4个 |
下列各式计算结果正确的是( )
| A、a3•a2=a6 |
| B、a3÷a2=a |
| C、(a3)2=a5 |
| D、2a2•(-a)=-2a2 |
 如图矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,DE的长为
如图矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,DE的长为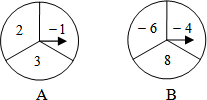 如图,有A、B两个可以自由转动的转盘,指针固定不动,转盘各被等分成三个扇形,并分别标上-1,2,3和-4,-6,8这6个数字.同时转动两个转盘各一次(指针落在等分线上时重转),转盘自由停止后,A转盘中指针指向的数字记为x,B转盘中指针指向的数字记为y,且m=xy.
如图,有A、B两个可以自由转动的转盘,指针固定不动,转盘各被等分成三个扇形,并分别标上-1,2,3和-4,-6,8这6个数字.同时转动两个转盘各一次(指针落在等分线上时重转),转盘自由停止后,A转盘中指针指向的数字记为x,B转盘中指针指向的数字记为y,且m=xy.
 在中俄“海上联合-2014”反潜演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,
在中俄“海上联合-2014”反潜演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5, 如图,AB∥CD,AB=CD,点E、F在BC上,且BF=CE,求证:△ABE≌△DCF.
如图,AB∥CD,AB=CD,点E、F在BC上,且BF=CE,求证:△ABE≌△DCF.