Question

20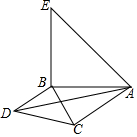．已知，如图，在△ABC中，∠BAC=45°，以B为直角顶点分别作Rt△BCD、Rt△BAE，且BC=BD，BA=BE，连接AD．猜想并证明线段AB、AD、AC之间的数量关系．

Answer 1

分析 结论：AC²+2AB²=AD²．由△ABD≌△EBC，推出AD=EC，由BA=BE，∠ABE=90°，推出∠BAE=45°，AE=$\sqrt{2}$AB，由∠BAC=45°，推出∠EAC=90°，推出AC²+AE²=EC²，由此即可证明．

解答 解：结论：AC²+2AB²=AD²．理由如下：
如图，连接EC．

∵∠ABE=∠DBC=90°，
∴∠EBC=∠ABD，
在△ABD和△EBC中，
$\left\{\begin{array}{l}{AB=EB}\\{∠ABD=∠EBC}\\{BD=BC}\end{array}\right.$，
∴△ABD≌△EBC，
∴AD=EC，
∵BA=BE，∠ABE=90°，
∴∠BAE=45°，AE=$\sqrt{2}$AB，
∵∠BAC=45°，
∴∠EAC=90°，
∴AC²+AE²=EC²，
∴AC²+2AB²=AD²．

点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质、勾股定理等知识，解题的关键是正确寻找全等三角形，灵活运用勾股定理解决问题，属于中考常考题型．