题目内容
 如图,某渔船在A处观测到灯塔M在它的北偏东48°方向上,这艘渔船以每小时28海里的速度向正东方向航行,半小时后到达B处,在B处观测到灯塔M在它的北偏东37°方向上.求B处与灯塔M的距离是多少海里?
如图,某渔船在A处观测到灯塔M在它的北偏东48°方向上,这艘渔船以每小时28海里的速度向正东方向航行,半小时后到达B处,在B处观测到灯塔M在它的北偏东37°方向上.求B处与灯塔M的距离是多少海里?(参考数据:sin37°≈
| 3 |
| 5 |
| 3 |
| 4 |
| 7 |
| 10 |
| 11 |
| 10 |
cos37°≈
| 4 |
| 5 |
| 7 |
| 11 |
考点:解直角三角形的应用-方向角问题
专题:
分析:过点M作MC⊥AB交延长线于点C,在Rt△AMC中,AC=
x;在Rt△BMC中,BC=
x;由于AC-BC=AB得关于x的方程,解方程得到x的值,再在Rt△BMC中,根据三角函数得到BM的长.
| 11 |
| 10 |
| 3 |
| 4 |
解答: 解:过点M作直线AB的垂线MC,垂足为C,设CM=x海里,
解:过点M作直线AB的垂线MC,垂足为C,设CM=x海里,
在Rt△AMC中,AC=
x;
在Rt△BMC中,BC=
x;
由于AC-BC=AB得:14=
x,
解得:x=40,
在Rt△BMC中,BM=MC÷cos37°≈40÷
=50海里.
答:灯塔B与渔船M的距离是50海里.
 解:过点M作直线AB的垂线MC,垂足为C,设CM=x海里,
解:过点M作直线AB的垂线MC,垂足为C,设CM=x海里,在Rt△AMC中,AC=
| 11 |
| 10 |
在Rt△BMC中,BC=
| 3 |
| 4 |
由于AC-BC=AB得:14=
| 7 |
| 20 |
解得:x=40,
在Rt△BMC中,BM=MC÷cos37°≈40÷
| 4 |
| 5 |
答:灯塔B与渔船M的距离是50海里.
点评:考查了解直角三角形的应用-方向角问题.解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
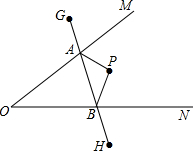 如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若GH的长为10cm,求△PAB的周长为( )
如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若GH的长为10cm,求△PAB的周长为( )| A、5cm | B、10cm |
| C、20cm | D、15cm |
已知y=-
,下列结论中,错误的是( )
| 2 |
| x |
| A、图象必经过(-1,2) |
| B、y随x的增大而增大 |
| C、图象位于第二、四象限内 |
| D、若x>1,则-2<y<0 |
 如图,△ABC中,BO平分∠ABC,CO平分∠ACB,MN经过点O且MN∥BC,若AB=12,AC=18,求△AMN的周长.
如图,△ABC中,BO平分∠ABC,CO平分∠ACB,MN经过点O且MN∥BC,若AB=12,AC=18,求△AMN的周长. 如图,点E、C在线段BF上,且BE=CF,AB
如图,点E、C在线段BF上,且BE=CF,AB