题目内容
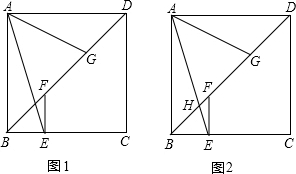
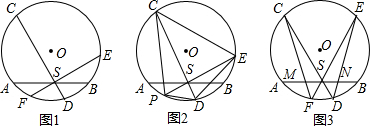
12.已知,如图正方形ABCD中,E为BC上任意一点,过E作EF⊥BC,交BD于F,G为DF的中点,连AE和AG.(1)如图1,求证:∠FEA+∠DAG=45°;
(2)如图2在(1)的条件下,设BD和AE的交点为H,BG=8,DH=9,求AD的长.
分析 (1)作GM⊥BC于M,连接GE、GC,如图1,由正方形的性质得DA=DC,∠ADB=∠CDB=45°,再证明△ADG≌△CDG得到AG=CG,∠DAG=∠1,∠AGD=∠CGD,接着利用等腰三角形的判定与性质得到GC=GE,∠5=∠4,∠2=∠3,从而得到∠1=∠6=∠DAG,GA=GE,再证明△AGE为等腰直角三角形得到∠AEG=45°,从而得到∠FEA+∠DAG=45°;
(2)把△ADG绕点A顺时针旋转90°得到△ABQ,连接QH,如图2,利用旋转的性质得∠ABQ=∠ABD=45°,AQ=AD,BQ=DG,∠QAG=90°,再证明△QAH≌△GAH得到HQ=HG,设BH=x,用x表示出则HG=HQ=8-x,BQ=x+1,然后在Rt△BQH中利用勾股定理得到(x+1)2+x2=(8-x)2,解得x=3,则BD=BH+DH=12,然后根据等腰直角三角形的性质求AD.
解答 (1)证明:作GM⊥BC于M,连接GE、GC,如图1,
∵四边形ABCD为正方形,
∴DA=DC,∠ADB=∠CDB=45°,
在△ADG和△CDG中
$\left\{\begin{array}{l}{DA=DC}\\{∠ADG=∠CDG}\\{DG=DG}\end{array}\right.$,
∴△ADG≌△CDG,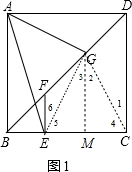
∴AG=CG,∠DAG=∠1,∠AGD=∠CGD,
∵G点为DF的中点,FE⊥BC,GM⊥BC,DC⊥BC,
∴GM为梯形CDFE的中位线,
∴EM=CM,
∴GE=GC,∠5=∠4,
∴GM平分∠EGC,
∴∠2=∠3,
∴∠1=∠6=∠DAG,GA=GE,
∵GM∥CD,
∴∠MGD=180°-∠GDC=135°,即∠2+∠DGC=135°,
∴∠AGD+∠3=∠2+∠DGC=135°,
∴∠AGE=90°,
∴△AGE为等腰直角三角形,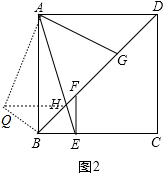
∴∠AEG=45°,即∠FEA+∠6=45°,
∴∠FEA+∠DAG=45°;
(2)解:把△ADG绕点A顺时针旋转90°得到△ABQ,连接QH,如图2,
∴∠ABQ=∠ABD=45°,AQ=AD,BQ=DG,∠QAG=90°,
∵∠FEA+∠DAG=45°;
而∠FEA=∠BAE,
∴∠BAE+∠DAG=45°;
∴∠EAG=45°,
∴∠QAE=45°,
在△QAH和△GAH中
$\left\{\begin{array}{l}{AQ=AG}\\{∠QAH=∠GAH}\\{AH=AH}\end{array}\right.$,
∴△QAH≌△GAH,
∴HQ=HG,
设BH=x,则HG=BG-BH=8-x,
∴HQ=8-x,
∵DH=BG+DG-BH,
∴DG=9-8+x=x+1,
∴BQ=x+1,
∵∠ABQ+∠ABD=45°+45°=90°,
∴△BQH为直角三角形,
∴BQ2+BH2=QH2,即(x+1)2+x2=(8-x)2,解得x=3,
∴BD=BH+DH=3+9=12,
∴AD=$\frac{\sqrt{2}}{2}$BD=6$\sqrt{2}$.
点评 本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.解决问题的关键是全等三角形和直角三角形.

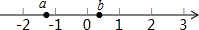 已知a、b在数轴上的位置如图,则a+b,a-b,b-a,-a-b中,最大的数是哪一个?
已知a、b在数轴上的位置如图,则a+b,a-b,b-a,-a-b中,最大的数是哪一个? 如图,有一块三角形材料(△ABC),请你画出一个半圆,使得圆心在线段AC上,且与AB、BC相切.
如图,有一块三角形材料(△ABC),请你画出一个半圆,使得圆心在线段AC上,且与AB、BC相切.
 如图所示,直线y=x+2与x轴交于点A,与y轴交于点B,AB⊥BC,且点C在x轴上,若抛物线y=ax2+bx+c以C为顶点,且经过点B,求这条抛物线的解析式.
如图所示,直线y=x+2与x轴交于点A,与y轴交于点B,AB⊥BC,且点C在x轴上,若抛物线y=ax2+bx+c以C为顶点,且经过点B,求这条抛物线的解析式.