题目内容
 如图,平行四边形ABCD中,AE、DF分别是∠BAD、∠ADC的角平分线,相交于点G,交BC边于E、F点,已知AD=8,EF=2,则平行四边形AB长为( )
如图,平行四边形ABCD中,AE、DF分别是∠BAD、∠ADC的角平分线,相交于点G,交BC边于E、F点,已知AD=8,EF=2,则平行四边形AB长为( )| A、3 | B、4 | C、5 | D、6 |
考点:平行四边形的性质
专题:
分析:首先判断BA=BE=CF=CD,从而求出BF,得出BE的长,即可得出答案.
解答:解:∵AE、DF分别是∠BAD、∠ADC的角平分线,
∴∠BAE=∠DAE,∠CDF=∠ADF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠DAE=∠BEA,∠ADF=∠CFD,
∴∠BAE=∠BEA,∠CFD=∠CDF,
∴BE=BA=CF=CD,
又∵AD=8,EF=2,
∴BF=
(BC-EF)=3,
∴BE=BF+EF=5,
∴AB=5.
故选C.
∴∠BAE=∠DAE,∠CDF=∠ADF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠DAE=∠BEA,∠ADF=∠CFD,
∴∠BAE=∠BEA,∠CFD=∠CDF,
∴BE=BA=CF=CD,
又∵AD=8,EF=2,
∴BF=
| 1 |
| 2 |
∴BE=BF+EF=5,
∴AB=5.
故选C.
点评:本题考查了平行四边形的性质,解答本题的关键是判断出BA=BE=CF=CD,难度一般.

练习册系列答案
相关题目
下列运算正确的是( )
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、|
|
已知关于x的不等式组
无解,则m取值范围是( )
|
| A、m<2 | B、m≤2 |
| C、m>2 | D、m≥2 |
函数y=
中,自变量x的取值范围是( )
| 3+x |
| A、x≥3 | B、x≤3 |
| C、x≥-3 | D、x≤-3 |
如果(am•b•bn)3=a6b15,那么m,n的值分别是( )
| A、2,4 | B、2,5 |
| C、3,5 | D、3,-5 |
方程
=
的解为( )
| 2 |
| x |
| 1 |
| 1-x |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
下面四个图形中,∠1与∠2是对顶角的图形是( )
A、 |
B、 |
C、 |
D、 |
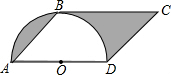 如图,已知?ABCD中,∠A=45°,AD=4cm,以AD为直径的半圆O与BC相切于点B,则图中阴影部分的面积是
如图,已知?ABCD中,∠A=45°,AD=4cm,以AD为直径的半圆O与BC相切于点B,则图中阴影部分的面积是