题目内容
 如图,在△ABC中,D,E,F分别为BC,AC,AB中点,求证:∠FDE=∠A.
如图,在△ABC中,D,E,F分别为BC,AC,AB中点,求证:∠FDE=∠A.考点:三角形中位线定理
专题:证明题
分析:由条件可知DF、DE为△ABC的中位线,可证明四边形AEDF为平行四边形,可得∠FDE=∠A.
解答:证明:∵D,E,F分别为BC,AC,AB中点,
∴DF、DE分别为△ABC的AC和AB边上的中位线,
∴DF∥AC,DE∥AB,
∴四边形AEDF是平行四边形,
∴∠FDE=∠A.
∴DF、DE分别为△ABC的AC和AB边上的中位线,
∴DF∥AC,DE∥AB,
∴四边形AEDF是平行四边形,
∴∠FDE=∠A.
点评:本题主要考查三角形中位线定理,掌握三角形中位线平行且等于第三边的一半是解题的关键

练习册系列答案
相关题目
下面两点中,关于x轴对称的是( )
| A、(3,-5)和(-3,-5) |
| B、(-1,3)和(1,-3) |
| C、(-2,4)和(2,-4) |
| D、(5,-3)和(5,3) |
现有一列式子:①552-452;②5552-4452;③55552-44452…则第⑧个式子的计算结果用科学记数法可表示为( )
| A、1.1111111×1016 |
| B、1.1111111×1027 |
| C、1.111111×1056 |
| D、1.111111×1017 |
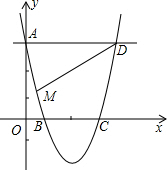 如图,已知点D(4,3)及经过A(0,3),B(1,0),C(3,0)三点的抛物线.
如图,已知点D(4,3)及经过A(0,3),B(1,0),C(3,0)三点的抛物线. 由16个相同的小正方形拼成的正方形网格,现将其中的两个小正方形涂黑.请你用两种不同的方法分别在图中再将两个空白的小正方形涂黑,使它成为轴对称图形.
由16个相同的小正方形拼成的正方形网格,现将其中的两个小正方形涂黑.请你用两种不同的方法分别在图中再将两个空白的小正方形涂黑,使它成为轴对称图形. 如图,正方形网格中的每个小正方形的边长都为1,每个小正方形的顶点叫格点,图中已给出了两个格点A,B,按要求画△ABC:使点C在格点上,且AC=5,BC=
如图,正方形网格中的每个小正方形的边长都为1,每个小正方形的顶点叫格点,图中已给出了两个格点A,B,按要求画△ABC:使点C在格点上,且AC=5,BC=