题目内容
在Rt△ACB中，∠C=90°，tanA=2
，则sinB=（ ）
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：互余两角三角函数的关系
专题：
分析：先根据题意设出直角三角形的两直角边，再根据勾股定理求出其斜边，运用三角函数的定义求解．
解答：解：∵在△ABC中，∠C=90°，tanA=2
，
设AC=x，则BC=2
x，
∴AB=
=5x．
∴sinB=
=
=
．
故选A．
| 6 |
设AC=x，则BC=2
| 6 |
∴AB=
| BC2+AC2 |
∴sinB=
| AC |
| AB |
| x |
| 5x |
| 1 |
| 5 |
故选A．
点评：本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．
练习册系列答案
相关题目
如图，图中已标出的8个角中，同位角、内错角、同旁内角各有几对？
观察图形并填空．
如图，AB与CD交于点O，OA=OC，OD=OB，∠A=50°，∠AOD=100°，则∠B的度数为（ ）| A、50° | B、30° |
| C、80° | D、100° |
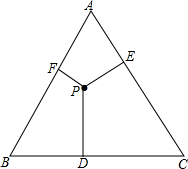△ABC是一个等边三角形，点P是△ABC内的一点，由P点分别向BC，CA和AB引垂线，PD，PE，PF，判断PD，PE，PF的和为常数吗？说明理由．