题目内容
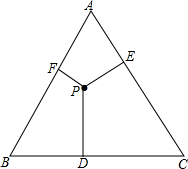 △ABC是一个等边三角形,点P是△ABC内的一点,由P点分别向BC,CA和AB引垂线,PD,PE,PF,判断PD,PE,PF的和为常数吗?说明理由.
△ABC是一个等边三角形,点P是△ABC内的一点,由P点分别向BC,CA和AB引垂线,PD,PE,PF,判断PD,PE,PF的和为常数吗?说明理由.考点:等边三角形的性质
专题:
分析:设△ABC的边长为a,求出等边三角形的高,再根据△ABC的面积等于△PAB、△PBC、△PAC三个三角形面积的和,列式并整理即可得到PD+PE+PF等于三角形的高.
解答:解:PD,PE,PF的和为常数.
理由:设△ABC的边长为a
∵正三角形的边长为a,
∴高为a×sin60°=
a,
∴S△ABC=
×a×
a=
a2,
∵PD、PE、PF分别为BC、AC、AB边上的高,
∴S△PBC=
BC•PD,S△PAC=
AC•PE,S△PAB=
AB•PF,
∵AB=BC=AC,
∴S△PBC+S△PAC+S△PAB=
BC•PD+
AC•PE+
AB•PF=
×2(PD+PE+PF)=PD+PE+PF,
∵S△ABC=S△PBC+S△PAC+S△PAB,
∴PD+PE+PF=
a,
∴PD,PE,PF的和为常数.
理由:设△ABC的边长为a
∵正三角形的边长为a,
∴高为a×sin60°=
| ||
| 2 |
∴S△ABC=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
∵PD、PE、PF分别为BC、AC、AB边上的高,
∴S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=BC=AC,
∴S△PBC+S△PAC+S△PAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵S△ABC=S△PBC+S△PAC+S△PAB,
∴PD+PE+PF=
| ||
| 2 |
∴PD,PE,PF的和为常数.
点评:本题考查的是等边三角形的性质,主要利用等边三角形三边相等的性质和三角形的面积等于被分体现了数学问题中由一般到特殊的解题思想.

练习册系列答案
相关题目
在Rt△ACB中,∠C=90°,tanA=2
,则sinB=( )
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
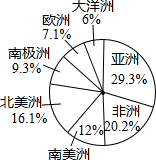 如图反映的是地球上七大洲的面积占陆地总面积的百分比,小明根据如图得出了
如图反映的是地球上七大洲的面积占陆地总面积的百分比,小明根据如图得出了下列四个结论:
①七大洲中面积最大的是亚洲;
②南美洲、北美洲、非洲三大州的面积和约占陆地总面积的50%;
③非洲约占陆地总面积的20%;
④南美洲的面积是大洋洲面积的2倍.
你认为上述四个结论中正确的应该是( )
| A、①② | B、①④ |
| C、①②④ | D、①②③④ |
若一个多边形的每个外角都为30°,则这个多边形是( )
| A、十二边形 | B、十边形 |
| C、八边形 | D、六边形 |
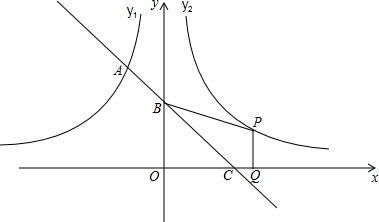
 如图,分别画出点A、B、C到BC、AC、AB的垂线段,并量出点A到BC,点B到AC,点C到AB的距离.
如图,分别画出点A、B、C到BC、AC、AB的垂线段,并量出点A到BC,点B到AC,点C到AB的距离.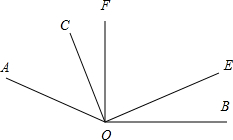 已知∠AOB=160°,∠COE=180°,OF平分∠AOE.如图,若∠COF=14°,则∠BOE=
已知∠AOB=160°,∠COE=180°,OF平分∠AOE.如图,若∠COF=14°,则∠BOE=