题目内容
13.如图,边长为4的等边三角形AOB的顶点O在坐标原点,点A在x轴的正半轴上,点B在第一象限.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段BP的中点绕点P按顺时针方向旋转60°得点C,点C随点P的运动而运动,连接CP、CA.过点P作PD⊥OB于D点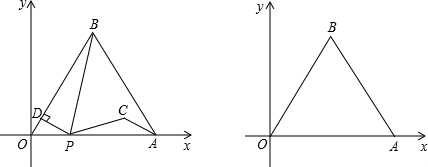
(1)直接写出BD的长并求出点C的坐标(用含t的代数式表示)
(2)在点P从O向A运动的过程中,△PCA能否成为直角三角形?若能,求t的值.若不能,请说明理由;
(3)点P从点O运动到点A时,点C运动路线的长是多少?
分析 (1)由三角形AOB是等边三角形可以得出OB=OA=AB=4,∠BOA=∠OAB=∠ABO=60°,由PD⊥OB就可以得出∠PDO=90°,再通过解直角三角形就可以用t把PD以及DP表示出来.再过C作CE⊥OA于E,可得△PCE∽△BPD,利用三角形相似的性质就可以CE和PE的值,从而可以表示出C的坐标;
(2)在P的移动过程中使△PCA为直角三角形分两种情况,当∠PCA=90°或∠PAC=90°时就可以求出相对应的t值;
(3)设C点的坐标,表示出坐标的函数关系式确定C的运动轨迹的图象为线段,再根据条件就可以求出起点的坐标和终点的坐标,运用两点间的距离公式就可以求出其值.
解答 解:(1)∵△AOB是等边三角形,
∴OB=OA=AB=4,∠BOA=∠OAB=∠ABO=60°.
∵PD⊥OB,
∴∠PDO=90°,
∴∠OPD=30°,
∴OD=$\frac{1}{2}$OP.
∵OP=t,
∴OD=$\frac{1}{2}$t,
∴BD=4-$\frac{1}{2}$t.
在Rt△OPD中,由勾股定理,得PD=$\frac{\sqrt{3}}{2}$t,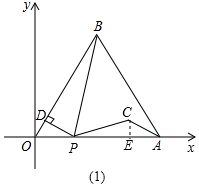
如图1,过C作CE⊥OA于E,则∠PEC=90°,
∵线段BP的中点绕点P按顺时针方向旋转60°得点C,
∴∠BPC=60°.
∵∠OPD=30°,
∴∠BPD+∠CPE=90°.
∴∠DBP=∠CPE
∴△PCE∽△BPD,
∴$\frac{CE}{PD}$=$\frac{PC}{PB}$=$\frac{PE}{BD}$,
∴$\frac{CE}{\frac{1}{2}\sqrt{3}t}$=$\frac{1}{2}$=$\frac{PE}{4-\frac{1}{2}t}$,
∴CE=$\frac{\sqrt{3}}{4}t$,PE=2-$\frac{1}{4}t$,
∴OE=OP+PE=2+$\frac{3}{4}t$,
∴C(2+$\frac{3}{4}t$,$\frac{\sqrt{3}}{4}t$).
(2)如图3,当∠PCA=90度时,作CF⊥PA,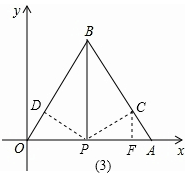
∴△PCF∽△ACF,
∴$\frac{PF}{CF}$=$\frac{CF}{AF}$,
∴CF2=PF•AF,
∵PF=2-$\frac{1}{4}$t,AF=4-OF=2-$\frac{3}{4}$t,CF=$\frac{\sqrt{3}}{4}$t,
∴($\frac{\sqrt{3}}{4}$t)2=(2-$\frac{1}{4}$t)(2-$\frac{3}{4}$t),
解得t=2,
此时P是OA的中点.
如图2,当∠CAP=90°时,C的横坐标就是4,
∴2+$\frac{3}{4}$t=4,
解得t=$\frac{8}{3}$;
(3)设C(x,y),
∴x=2+$\frac{3}{4}$t,y=$\frac{\sqrt{3}}{4}$t,
∴y=$\frac{\sqrt{3}}{3}$x-$\frac{8}{3}\sqrt{3}$,
∴C点的运动痕迹是一条线段(0≤t≤4).
当t=0时,C1(2,0),
当t=4时,C2(5,$\sqrt{3}$),
∴由两点间的距离公式得:C1C2=2$\sqrt{3}$.
故点C运动路线的长为:2$\sqrt{3}$.
点评 本题属于几何变换综合题,主要考查了相似三角形的判定与性质,勾股定理的运用,等边三角形的性质,直角三角形的性质,旋转的性质,两点间的距离公式的运用.解决问题的关键是依据相似三角形对应边成比例列出比例式进行计算求解.

| A. | a3+a2 | B. | a3•a2 | C. | (a3)2 | D. | a10÷a2 |
| A. | $\frac{100}{250}$(1+x)2=$\frac{736}{400}$ | B. | 100(1+x)2=736 | ||
| C. | 250(1+x)2=100 | D. | $\frac{736}{400}$(1-x)2=$\frac{100}{250}$ |
| A. | y(x2-4) | B. | y(x-2)2 | C. | y(x+4)(x-4) | D. | y(x+2)(x-2) |
 某商家为了给新产品作宜传,向全社会征集广告用语及商标图案,结果如图所示的商标(图中阴影部分)中标,求此商标图案的面积.(虚线左边为扇形,右边为长方形)
某商家为了给新产品作宜传,向全社会征集广告用语及商标图案,结果如图所示的商标(图中阴影部分)中标,求此商标图案的面积.(虚线左边为扇形,右边为长方形) 如图,已知AB为⊙O直径,过⊙O上一点C作⊙O的切线,交AB延长线于点E,作AD⊥CE,交EC延长线于D,交⊙O于点F,设∠ABC=α(0°<α<90°).
如图,已知AB为⊙O直径,过⊙O上一点C作⊙O的切线,交AB延长线于点E,作AD⊥CE,交EC延长线于D,交⊙O于点F,设∠ABC=α(0°<α<90°).
 如图,抛物线y=ax2+bx-3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,点M为该抛物线的顶点,连接BC、CM、BM.
如图,抛物线y=ax2+bx-3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,点M为该抛物线的顶点,连接BC、CM、BM.