题目内容
已知:如图,四边形ABCD为平行四边形,以CD为直径作⊙O,⊙O与边BC相交于点F,⊙O的切线DE与边AB相交于点E,且AE=3EB.
(1)求证:△ADE∽△CDF;
(2)当CF:FB=1:2时,求⊙O与▱ABCD的面积之比.
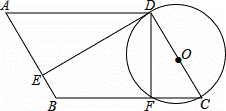
(1)证明:∵CD是⊙O的直径,
∴∠DFC=90°,
∵四边形ABCD是平行四边形,
∴∠A=∠C,AD∥BC,AB∥CD,
∴∠ADF=∠DFC=90°,
∵DE为⊙O的 切线,
切线,
∴DE⊥DC,
∴DE⊥AB,
∴∠DEA=∠DFC=90°,
∵∠A=∠C,
∴△ADE∽△CDF;
(2)解:∵CF:FB=1:2,
∴设CF=x,FB=2x,则BC=3x,
∵AE=3EB,
∴设EB=y,则AE=3y,AB=4y,
∵四边形ABCD是平行四边形 ,
,
∴AD=BC=3x,AB=DC=4y,
∵△ADE∽△CDF,
∴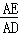 =
=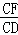 ,
,
∴ =
=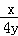 ,
,
∵x、y均为正数,
∴x=2y,
∴BC=6y,CF=2y,
在Rt△DFC中,∠DFC=90°,
由勾股定理得:DF=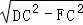 =
= =2
=2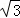 y,
y,
∴⊙O的面积为π•(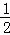 DC)2=
DC)2=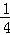 π•DC2=
π•DC2=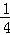
 π(4y)2=4πy2,
π(4y)2=4πy2,
四边形ABCD的面积为BC•DF=6y•2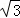 y=12
y=12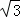 y2,
y2,
∴⊙O与四边形ABCD的面积之比为4πy2:12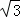 y2=π:3
y2=π:3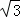 .
.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 G,且菱形AEFG∽菱形ABCD,连接EB,GD.
G,且菱形AEFG∽菱形ABCD,连接EB,GD.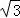 ,求GD的长.
,求GD的长.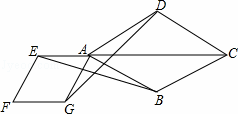
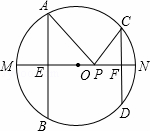


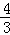 ,BE=7
,BE=7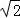 ,求线段PC的长.
,求线段PC的长.
 ,则tanB的值为( )
,则tanB的值为( ) B.
B. C.
C. D.
D. 
 ,AD=1.求BC的长.
,AD=1.求BC的长.