题目内容
1．已知方程组$\left\{\begin{array}{l}{4x-3y-3z=0}\\{x-3y+2z=0}\end{array}\right.$且z≠0，则x：y=15：11．分析 把z当成已知数，解关于x、y的方程组，求出方程组的解，再代入即可得出答案．
解答 解：$\left\{\begin{array}{l}{4x-3y-3z=0}\\{x-3y+2z=0}\end{array}\right.$
即$\left\{\begin{array}{l}{4x-3y=3z①}\\{x-3y=-2z②}\end{array}\right.$
①-②得：3x=5z，
解得：x=$\frac{5}{3}$z，
①-②×4得：9y=11z，
解得：y=$\frac{11}{9}$z，
所以x：y=15：11，
故答案为：15：11．
点评 本题考查了解三元一次方程组的应用，解此题的关键是求出x、y的值，即把z当作已知数求出x、y的值，难度适中．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
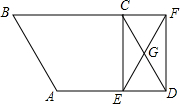如图，点E是平行四边形ABCD边AD上的一点，点G是CD的中点，连接EG并延长，交BC延长线于F，连接CE、DF．求证：四边形CEDF是平行四边形．
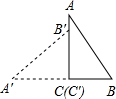如图，△ABC中，∠ACB=90°，AB=5，AC=4，将△ABC绕点C沿逆时针方向旋转90°得到的△A′B′C′沿CB向右平移，使点B′刚好落在AB边上，则△A′B′C′向右平移的距离是$\frac{3}{4}$．
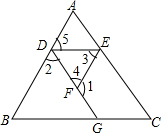如图所示，已知∠1+∠2=180°，∠3=∠B．