题目内容
8.若关于x的一元二次方程x2-2x+$\frac{1}{4}$m+3=0有两个不相等的实数根,则m的最大整数值是( )| A. | -9 | B. | -8 | C. | -7 | D. | -6 |
分析 根据方程的系数结合根的判别式即可得出关于m的一元一次不等式,解之即可得出m的取值范围,再取其内的最大整数值即可.
解答 解:∵关于x的一元二次方程x2-2x+$\frac{1}{4}$m+3=0有两个不相等的实数根,
∴△=(-2)2-4($\frac{1}{4}$m+3)=-m-8>0,
解得:m<-8,
∴m的最大整数值是-9.
故选A.
点评 本题考查了根的判别式,熟练掌握“当△>0时,方程有两个不相等的实数根”是解题的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
18.某天的温度上升了-3℃的意义是( )
| A. | 上升了3℃ | B. | 没有变化 | C. | 下降了-3℃ | D. | 下降了3℃ |
16.下列计算正确的是( )
| A. | 4x2-2x2=2 | B. | x+x=x2 | C. | 4x6÷2x2=2x3 | D. | x•x2=x3 |
3.比2的相反数小的是( )
| A. | 5 | B. | -3 | C. | 0 | D. | -1 |
13.下列几何体中,正视图是矩形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.若(a+$\sqrt{2}$)2与|b+1-$\sqrt{2}$|互为相反数,则a+b的值为( )
| A. | -1 | B. | 1 | C. | 2$\sqrt{2}$-1 | D. | 2$\sqrt{2}$+1 |
12.已知,k=$\frac{a+b-c}{c}$=$\frac{a-b+c}{b}$=$\frac{b+c-a}{a}$,则k的值为( )
| A. | $\frac{2}{3}$ | B. | 3 | C. | 1或-2 | D. | $\frac{3}{2}$ |
13.下列叙述正确的是( )
| A. | 平分弦的直径垂直于弦 | B. | 三角形的外心到三边的距离相等 | ||
| C. | 三角形的内心到三边的距离相等 | D. | 相等的圆周角所对的弧相等 |
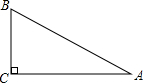 如图,台风过后,学校的旗杆在B处断裂,旗杆的顶部A落在离旗杆底部C6m处,已知旗杆长16m,则旗杆是在距离底部8m处断裂的.
如图,台风过后,学校的旗杆在B处断裂,旗杆的顶部A落在离旗杆底部C6m处,已知旗杆长16m,则旗杆是在距离底部8m处断裂的.