题目内容
17.如果圆的最大弦长是m,直线与圆心的距离为d,且直线与圆相离,那么( )| A. | d>m | B. | d>$\frac{1}{2}$m | C. | d≥$\frac{1}{2}$m | D. | d≤$\frac{1}{2}$m |
分析 已知圆的半径是R,圆心到直线l的距离是d,那么①当d<R时,直线l和圆的位置关系是相交;②当d=R时,直线l和圆的位置关系是相切;③当d>R时,直线l和圆的位置关系是相离,根据以上内容求出即可.
解答 解:∵如果圆的最大弦长是m,
圆的半径为$\frac{1}{2}$m,直线和圆相离,
∴圆心到直线的距离d的取值范围是d>$\frac{1}{2}$m,
故选B.
点评 本题考查了直线与圆的位置关系的应用,注意:已知圆的半径是R,圆心到直线l的距离是d,那么①当d<R时,直线l和圆的位置关系是相交;②当d=R时,直线l和圆的位置关系是相切;③当d>R时,直线l和圆的位置关系是相离.

练习册系列答案
相关题目
7.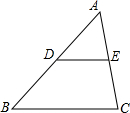 如图,△ABC中,点D,E分别是AB、AC的中点,下列结论不正确的是( )
如图,△ABC中,点D,E分别是AB、AC的中点,下列结论不正确的是( )
 如图,△ABC中,点D,E分别是AB、AC的中点,下列结论不正确的是( )
如图,△ABC中,点D,E分别是AB、AC的中点,下列结论不正确的是( )| A. | BC=2DE | B. | △ADE∽△ABC | C. | $\frac{AD}{AE}$=$\frac{AB}{AC}$ | D. | S△ABC=2S△ADE |
8.若w=9-($\frac{n}{m}$+1)2,当W有最大值为P时,则3P+2m+2n的值为( )
| A. | 25 | B. | 27 | C. | 9 | D. | 不能确定 |
5.下列计算正确的是( )
| A. | $\frac{1}{a}+\frac{1}{a}=\frac{1}{2a}$ | B. | $\frac{1}{a-b}+\frac{1}{b-a}=0$ | ||
| C. | $\frac{m-n}{a}-\frac{m+n}{a}=0$ | D. | $\frac{1}{{{{(a-b)}^2}}}+\frac{1}{{{{(b-a)}^2}}}=\frac{1}{{{{(a-b)}^2}}}$ |
12.比-6大2的数是( )
| A. | -8 | B. | -4 | C. | 4 | D. | 8 |
2.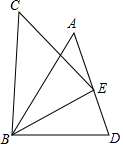 如图,已知,△ABD≌△CBE,下列结论不正确的是( )
如图,已知,△ABD≌△CBE,下列结论不正确的是( )
 如图,已知,△ABD≌△CBE,下列结论不正确的是( )
如图,已知,△ABD≌△CBE,下列结论不正确的是( )| A. | ∠CBE=∠ABD | B. | BE=BD | C. | ∠CEB=∠BDE | D. | AE=ED |
6.把(+12)-(-18)+(-7)+(-15)写成省略加号的和的形式是( )
| A. | 12-8-7+15 | B. | -12+18+7-15 | C. | 12+18+7-15 | D. | 12+18-7-15 |
 如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DM⊥AC交AC的延长线于M,连接CD,给出五个结论:①∠CAD=∠CBD;②S△DBC=S△AEC;③∠ADC=45°;④AC+CE=AB;⑤CE=2MC,其中正确的结论有( )
如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,DM⊥AC交AC的延长线于M,连接CD,给出五个结论:①∠CAD=∠CBD;②S△DBC=S△AEC;③∠ADC=45°;④AC+CE=AB;⑤CE=2MC,其中正确的结论有( )