题目内容
19.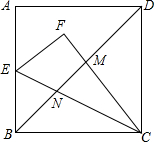 在正方形ABCD中,AD=4.点E是线段AB的中点,连接CE,将△BCE沿CE翻折,使点B落在点F处,对角线BD与CF,CE分别相交于点M,N,则MN的长是$\frac{20}{21}\sqrt{2}$..
在正方形ABCD中,AD=4.点E是线段AB的中点,连接CE,将△BCE沿CE翻折,使点B落在点F处,对角线BD与CF,CE分别相交于点M,N,则MN的长是$\frac{20}{21}\sqrt{2}$..
分析 先构造出直角三角形,利用三角函数求出BG=NE=$\frac{4}{3}$,CN=$\frac{4\sqrt{5}}{3}$,进而求出BN,再构造出等腰三角形,求出NH=CH=$\frac{5}{3}$,最后用平行线分线段成比例即可求出MN.
解答 解:如图,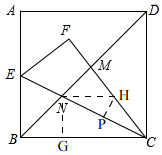
过点N作NG⊥BC,
∵点E是正方形的边AB中点,
∴BE=$\frac{1}{2}$AB=$\frac{1}{2}$BC,
∴tan∠BCE=$\frac{BE}{BC}$=$\frac{1}{2}$,
在Rt△CGN中,tan∠BCE=$\frac{NG}{CG}$,
∵BD是正方形ABCD的对角线,
∴∠CBD=45°,
∴NG=BG,CG=BC-BG=4-BG,
∴$\frac{BG}{4-BG}=\frac{1}{2}$,
∴NG=BG=$\frac{4}{3}$,
∴CG=$\frac{8}{3}$,
在Rt△CGN中,CN=$\sqrt{C{G}^{2}+N{G}^{2}}$=$\frac{4\sqrt{5}}{3}$
在Rt△BNG中,BN=$\sqrt{2}$BG=$\frac{4\sqrt{2}}{3}$,
过点N作NH∥BC,过点H作HP⊥CE,
由折叠得,∠BCE=∠FCE,
∴NH=CH,PN=PC=$\frac{1}{2}$CN=$\frac{2\sqrt{5}}{3}$,
∵tan∠PCH=$\frac{PH}{PC}=\frac{1}{2}$,
∴PH=$\frac{1}{2}$PC=$\frac{\sqrt{5}}{3}$,
根据勾股定理得,NH=CH=$\sqrt{P{H}^{2}+P{C}^{2}}$=$\frac{5}{3}$,
∵NH∥BC,
∴$\frac{MN}{BM}=\frac{NH}{BC}$,
∴$\frac{MN}{BN+MN}=\frac{NH}{BC}$,
∴$\frac{MN}{\frac{4\sqrt{2}}{3}+MN}=\frac{\frac{5}{3}}{4}$
∴MN=$\frac{20}{21}\sqrt{2}$.
故答案为$\frac{20}{21}\sqrt{2}$.
点评 此题是折叠问题,主要考查了正方形的性质,勾股定理,锐角三角函数,等腰三角形的性质和判定,解本题的关键是构造在出等腰三角形,注意:图形中有角平分线和平行线出现,易出现等腰三角形.

| A. | k>-1 | B. | k<1 | C. | k≥-l且k≠0 | D. | k<1且k≠0 |
| A. | 三角形的内心到三角形的三个顶点的距离相等 | |
| B. | 三点确定一个圆 | |
| C. | 垂直于半径的直线一定是这个圆的切线 | |
| D. | 任何三角形有且只有一个内切圆 |
| A. | x-y=6 | B. | x-$\frac{1}{2}$=$\frac{x-2}{3}$ | C. | 3x-4 | D. | x2+x=1 |
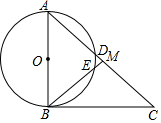 如图,在直角△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
如图,在直角△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.