题目内容
7. 如图△ABC为等腰直角三角形,其中∠A=90°,AB=AC=2,点D为BC中点,将一含45°角的三角板的一个锐角顶点落在点D处,三角板绕点D旋转,三角板两边分别与AB边与AC边交于点E、F两点.
如图△ABC为等腰直角三角形,其中∠A=90°,AB=AC=2,点D为BC中点,将一含45°角的三角板的一个锐角顶点落在点D处,三角板绕点D旋转,三角板两边分别与AB边与AC边交于点E、F两点.(1)求证:△BDE∽△CFD.
(2)△BDE和△EDF是否相似,若相似,请证明,若不相似,说明理由.
(3)若EF为x,△EDF的面积为y,求y与x的函数关系式.
分析 (1)找出△BDE与△CFD的对应角,其中∠BDE+∠CDF=135°,∠CDF+∠CFD=135°,得出∠BDE=∠CFD,从而解决问题;
(2)由(1)△BDE∽△CFD得出CD:BE=DF:DE,进而得出 DB:BE=DF:DE即可得出结论;
(3)由(2)得出对应边成比例,和三角形的面积公式求解即可.
解答 (1)证明:∵在△ABC中,∠BAC=90°,AB=AC,
∴∠B=∠C=45°.
∵∠B+∠BDE+∠BED=180°,
∴∠BDE+∠BED=135°,
∵∠EDF=45°,
又∵∠BDE+∠EDF+∠CDF=180°,
∴∠BDE+∠CDF=135°,
∴∠BED=∠CDF,
又∵∠B=∠C,
∴△BDE∽△CFD(两角对应相等的两个三角形相似);
(2)△BDE∽△DFE
理由:由(1)知,△BDE∽△CFD,
得 CD:BE=DF:DE,
而CD=BD,
∴DB:BE=DF:DE.
∵∠EBD=∠EDF,
∴△BDE∽△DFE(两边对应成比例且夹角相等的两个三角形相似).
(3)△ABC为等腰直角三角形,且AB=AC=2,D为BC中点,
∴BD=$\sqrt{2}$.
设ED=y,
∵△BDE∽△DFE,
∴$\frac{ED}{BE}=\frac{FD}{BD}=\frac{FE}{ED}$,
即 $\frac{y}{BE}=\frac{FD}{\sqrt{2}}=\frac{x}{y}$,
解得:FD=$\frac{\sqrt{2}x}{y}$,
则S△EDF=$\frac{1}{2}$•sin45°•ED•FD=$\frac{\sqrt{2}}{4}$•ED•FD.
∵ED•FD=$\sqrt{2}$x.
∴S=$\frac{1}{2}$x
点评 此题主要考查了相似三角形的判定.它以每位学生都有的三角板在图形上的运动为背景,既考查了学生图形旋转变换的思想,静中思动,动中求静的思维方法,又考查了学生动手实践、自主探究的能力

 活力课时同步练习册系列答案
活力课时同步练习册系列答案| A. | 图象经过第二象限 | B. | 函数值y随x的增大而减小 | ||
| C. | 图象在x轴上的截距是1 | D. | 图象在y轴上的截距是-1 |
| A. | $\sqrt{16}$=±4 | B. | $\root{3}{27}$=-3 | C. | ±$\sqrt{16}$=4 | D. | $\sqrt{(-4)^{3}}$=-4 |
①一对有序实数对
②到原点的距离为5北偏东45°的方向
③到原点的距离为5,西南方向
④东偏南37°
⑤北纬40o,东经116o.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
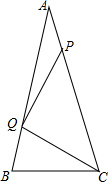 如图所示,在△ABC中,AB=AC,∠BAC=30°,P、Q分别为AB、AC的点,且∠QPC=45°,PQ=BC,证明:BC=CQ.
如图所示,在△ABC中,AB=AC,∠BAC=30°,P、Q分别为AB、AC的点,且∠QPC=45°,PQ=BC,证明:BC=CQ.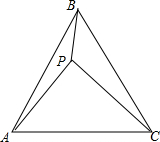 如图,△ABC是等边三角形,P是△ABC内一点,且满足PA2+PB2=PC2.
如图,△ABC是等边三角形,P是△ABC内一点,且满足PA2+PB2=PC2.