题目内容

精英家教网如图，在△ADC中，EF∥BC，S△AEF=S四边形BCEF，则AE：AB等于（　　）
A、
1
4
B、
1
3
C、
2
2
D、
3
2
分析：根据EF∥BC可以求得
AE
AB
=
AF
AC
，根据S△AEF=S四边形BCEF可以求得S△AEF=
1
2
S△ABC，即可得
AE
AB
，即可解题．
解答：解：∵S△AEF=S四边形BCEF，
∴S△AEF=
1
2
S△ABC
∴2×
1
2
AE•AF•sinA=
1
2
AB•AC•sinA
又∵EF∥BC
∴
AE
AB
=
AF
AC

∴
AE
AB
=
AF
AC
=
2
2
．
故选 C．
点评：本题考查了三角形面积的计算，考查了平行线定理，考查了相似三角形对应边比值相等的性质，本题中根据
AE
AB
=
AF
AC
求值是解题的关键．
练习册系列答案
相关题目
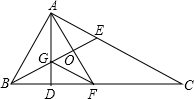精英家教网如图，在△ADC中，∠BAC=90°，AD⊥BC，BE、AF分别是∠ABC、∠DAC的平分线，BE和AD交于G，求证：GF∥AC．
已知，如图，在△ADC中，∠ADC=90°，以DC为直径作半圆⊙O，交边AC于点F，点B在CD的延长线上，连接BF，交AD于点E，∠BED=2∠C．
（1）求证：BF是⊙O的切线；
（2）若BF=FC，AE=
3
，求⊙O的半径．
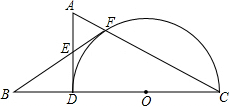已知，如图，在△ADC中，∠ADC=90°，∠A=60°，以DC为直径作半圆⊙O，交边AC于点F，点B在CD的延长线上，连接BF，交AD于点E，BF=FC．
（1）求证：BF是⊙O的切线；
（2）若AE=
3
，求⊙O的半径．
如图，在△ADC中，AD，BE分别为边BC，AC上的高，D，E为垂足，M为AB的中点，N为DE的中点，求证：
（1）△MDE是等腰三角形；
（2）MN⊥DE．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网