题目内容
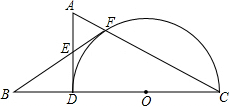 已知,如图,在△ADC中,∠ADC=90°,∠A=60°,以DC为直径作半圆⊙O,交边AC于点F,点B在CD的延长线上,连接BF,交AD于点E,BF=FC.
已知,如图,在△ADC中,∠ADC=90°,∠A=60°,以DC为直径作半圆⊙O,交边AC于点F,点B在CD的延长线上,连接BF,交AD于点E,BF=FC.(1)求证:BF是⊙O的切线;
(2)若AE=
| 3 |
分析:(1)连接OF,先根据三角形内角和定理计算出∠C=30°,再根据三角形外角性质得到∠BOF=∠C+∠OCF=60°,由BF=FC得到∠B=∠C=30°,则可计算出∠OFB=90°,然后根据切线的判定定理得到结论;
(2)先证明△AEF是等边三角形,则EF=AE=
,再证明AD为⊙O切线,根据切线长定理得到EF=ED=
,所以AD=2
,然后根据含30度的直角三角形三边的关系得到CD=
AD=6,即可得到⊙O的半径是3.
(2)先证明△AEF是等边三角形,则EF=AE=
| 3 |
| 3 |
| 3 |
| 3 |
解答: (1)证明:连接OF,如图,
(1)证明:连接OF,如图,
∵∠ADC=90°,∠A=60°
∴∠C=30°,
∵OC=OF,
∴∠C=∠OFC=30°,
∴∠BOF=∠C+∠OCF=60°,
∵BF=FC,
∴∠B=∠C=30°,
∴∠OFB=180°-∠B-∠BOF=90°,
∴OF⊥BF,
∴BF是⊙O的切线;
(2)解:∵∠AFE=∠B+∠C=60°,∠A=60°,
∴△AEF是等边三角形,
∴EF=AE=
,
∵∠ADC=90°,即OD⊥AD,
∴ED与⊙O相切于D,
∴EF=ED=
,
∴AD=2
,
∴CD=
AD=6,
∴⊙O的半径是3.
 (1)证明:连接OF,如图,
(1)证明:连接OF,如图,∵∠ADC=90°,∠A=60°
∴∠C=30°,
∵OC=OF,
∴∠C=∠OFC=30°,
∴∠BOF=∠C+∠OCF=60°,
∵BF=FC,
∴∠B=∠C=30°,
∴∠OFB=180°-∠B-∠BOF=90°,
∴OF⊥BF,
∴BF是⊙O的切线;
(2)解:∵∠AFE=∠B+∠C=60°,∠A=60°,
∴△AEF是等边三角形,
∴EF=AE=
| 3 |
∵∠ADC=90°,即OD⊥AD,
∴ED与⊙O相切于D,
∴EF=ED=
| 3 |
∴AD=2
| 3 |
∴CD=
| 3 |
∴⊙O的半径是3.
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了切线长定理和含30度的直角三角形三边的关系.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 9、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点P为BC边上一点,PE⊥AB,PF⊥CD,BG⊥CD,垂足分别为E、F、G.求证:PE+PF=BG.
9、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点P为BC边上一点,PE⊥AB,PF⊥CD,BG⊥CD,垂足分别为E、F、G.求证:PE+PF=BG. 求:(1)DE的长;(2)sin∠EDF的值.
求:(1)DE的长;(2)sin∠EDF的值. (2012•普陀区二模)已知:如图,在△ABC中,CD⊥AB,sinA=
(2012•普陀区二模)已知:如图,在△ABC中,CD⊥AB,sinA= 已知:如图,在△ABC中,D是BC边的中点,E是AD的中点,连接BE并延长到点F,使EF=BE,连接AF、CF.
已知:如图,在△ABC中,D是BC边的中点,E是AD的中点,连接BE并延长到点F,使EF=BE,连接AF、CF. 已知,如图,在四边形ABCD中,∠A=90°.若AB=4cm,AD=3cm,CD=12cm,BC=13cm,
已知,如图,在四边形ABCD中,∠A=90°.若AB=4cm,AD=3cm,CD=12cm,BC=13cm,