题目内容
 如图,在△ADC中,AD,BE分别为边BC,AC上的高,D,E为垂足,M为AB的中点,N为DE的中点,求证:
如图,在△ADC中,AD,BE分别为边BC,AC上的高,D,E为垂足,M为AB的中点,N为DE的中点,求证:(1)△MDE是等腰三角形;
(2)MN⊥DE.
分析:(1)由“直角三角形斜边上的中线等于斜边的一半”证得ME=MD=
AB;
(2)由等腰三角形的“三合一”的性质证得结论.
| 1 |
| 2 |
(2)由等腰三角形的“三合一”的性质证得结论.
解答:证明:(1)如图,在△ABD中,AD⊥BD,则△ABD是直角三角形,AB是斜边.
∵M是AB的中点,
∴MD=
AB.
同理,ME=
AB,
∴ME=MD,
∴△MDE是等腰三角形;
(2)由(1)知,△MDE是等腰三角形.
∵N是ED的中点,
∴MN平分DE,
∴MN⊥DE.
∵M是AB的中点,
∴MD=
| 1 |
| 2 |
同理,ME=
| 1 |
| 2 |
∴ME=MD,
∴△MDE是等腰三角形;
(2)由(1)知,△MDE是等腰三角形.
∵N是ED的中点,
∴MN平分DE,
∴MN⊥DE.
点评:本题考查了等腰三角形的判定与性质,直角三角形斜边上的中线.在直角三角形中,斜边上的中线等于斜边的一半.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 如图,在△ADC中,EF∥BC,S△AEF=S四边形BCEF,则AE:AB等于( )
如图,在△ADC中,EF∥BC,S△AEF=S四边形BCEF,则AE:AB等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
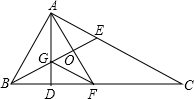 如图,在△ADC中,∠BAC=90°,AD⊥BC,BE、AF分别是∠ABC、∠DAC的平分线,BE和AD交于G,求证:GF∥AC.
如图,在△ADC中,∠BAC=90°,AD⊥BC,BE、AF分别是∠ABC、∠DAC的平分线,BE和AD交于G,求证:GF∥AC. 已知,如图,在△ADC中,∠ADC=90°,以DC为直径作半圆⊙O,交边AC于点F,点B在CD的延长线上,连接BF,交AD于点E,∠BED=2∠C.
已知,如图,在△ADC中,∠ADC=90°,以DC为直径作半圆⊙O,交边AC于点F,点B在CD的延长线上,连接BF,交AD于点E,∠BED=2∠C.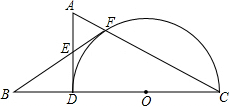 已知,如图,在△ADC中,∠ADC=90°,∠A=60°,以DC为直径作半圆⊙O,交边AC于点F,点B在CD的延长线上,连接BF,交AD于点E,BF=FC.
已知,如图,在△ADC中,∠ADC=90°,∠A=60°,以DC为直径作半圆⊙O,交边AC于点F,点B在CD的延长线上,连接BF,交AD于点E,BF=FC.